认识到自己的局限性,认识到了之后,也会变得对别人更加宽容。
本文是《Introduction to Software Testing》第六章“Input Space Partitioning”的笔记和总结。
1. 术语
- 输入域(Input Domain):程序所有可能的输入
- 输入参数:定义了输入域的范围,可能是
- 方法参数
- 非本地变量
- 用户输入
- 输入参数:定义了输入域的范围,可能是
- 域(Domain): D
- 划分(partition): q over D
- 划分必须满足两个属性
- 不相交性:块两两不相交
- 完整性:块的并组成了这个域D
- 划分必须满足两个属性
- 特征(characteristic): 不同的划分基于程序/参数(语法/语义)的不同的特征给出
- 显然测试输入可能满足多个特征
- 例如
- 是否为null
- 是否有序
- 输入设备文件的分类
1.1. 示例:考虑特征-文件的有序性
- b1: 文件内容升序
- b2: 文件内容降序
- b3: 文件内容任意序
但是若文件长度为1,明显各种特征均满足。
- 解决方案:每一个特征应该对应一个划分。为true为false各一次。
- 文件内容升序
- b1:true
- b2:false
- 文件内容降序
- b1:true
- b2:false
- 输入为null
- b1:true
- b2:false
- 文件内容升序
1.2. 划分的意义
- 通常使用划分q将输入域划分为块(block)集合
- $B_q = b_1, b_2, …, b_q$
- 使用一:独立考虑各个参数的域,将每个域划分为blocks,之后合并各个参数的blocks
- 使用二:考虑多个参数相互作用
- 我们认为同一特征下的参数取值是等价的
2. 输入域建模
输入域建模包括下面的步骤:
- 识别可测试的函数
- 找到所有参数
- 建模输入域(input domain model):测试人员需要
- 通过特征描述输入域的结构
- 为每一种特征创建一个划分(partition)
- 每一个划分是一个blocks集合,每一个block包含了等价的值集合。
- 测试输入需要为每一个输入参数赋一个值。由于不相交性,每一种特征测试输入仅对应一个block。
接着介绍两种建模输入域的方法。
2.1. 建模输入域的方法
- 基于接口(interface-based)
- 从单个输入参数获取特征
- 特点:忽略不同参数间的关系,独立考虑每个参数,大多依赖于语法
- 基于功能(functionality-based)
- 从被测程序的行为角度获取特征
- 特点:能够结合参数间关系,能够基于需求,能够结合语义和领域知识
2.2. 设计特征
- 基于接口设计特征
- 有效、无效和特殊值
- 域边界
- 基于功能设计特征
- 前置条件、后置条件
- 变量关系
- 变量能取到的特殊值
- 根据其它领域知识设计

2.3. 计算block以及对应的测试输入值的选取
特征设计好之后,需要考虑block如何划分和每个block有哪些可取的值的问题。
基于接口:

如图,对于特征1,可以选择side 1为7,0,-3即构成3个测试。
基于功能:
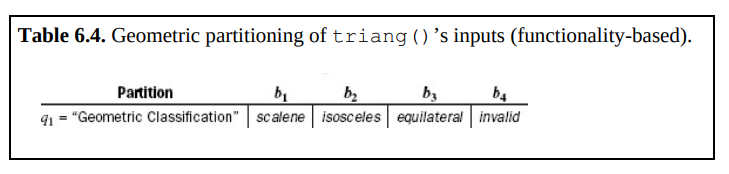
3. 覆盖准则
How should we consider multiple partitions at the same time?
多个特征的划分可以相结合的使用。也即构造满足多个特征不同block的测试输入。
- 用$q$表示特征数
- All Combinations(ACoC):所有特征的所有block组合
- 总数:$\prod_i^{q} B_i$
- 例如:[A, B], [1, 2, 3], [x, y]
- 有$232 = 12种$
- Each Choice(EC): 每一个特征的每一个block只需要满足一次
- 总数: $Max(B_1, B_2, …, B_q)$
- 例如:[A, B], [1, 2, 3], [x, y]
- (A, 1, x), (A, 2, y), (B, 3, x)即可满足
- Pair-Wise(PW): 每个特征的每个block的一个值必须和其它特征的每一个block组合
- 总数: $(Max_{i}(B_i)) * (Max_{j\ne i}(B_j))$
- 即两个最大的划分的block数的乘积
- 例如:[A, B], [1, 2, 3], [x, y]需要满足下面的组合
- (A, 1), (A, 2), (A, 3), (A, x), (A, y)
- (B, 1), (B, 2), (B, 3), (B, x), (B, y)
- (1, x), (1, y), (2, x), (2, y), (3, x), (3, y)
- 通过整合上述要求可以简化得到下面测试用例:
- (A, 1, x), (A, 2, y), (A, 3, x), (B, 1, y), (B, 2, x), (B, 3, y)
- 总数: $(Max_{i}(B_i)) * (Max_{j\ne i}(B_j))$
- T-Wise(TW): 每t个特征内的block必须组合在一起。
- 是t=2的扩展,同时若t取为特征数,则和ACoC等价
- 总数: 若每个特征/划分的block数相同,$(Max_{i=1}^qB_i)^t$
- 即最大的t个特征的block数的乘积
上面的覆盖准则无意识的将特征进行组合。
- Base Choice Coverage(BCC): 每个特征选择一个base choice block。base test通过使用每个特征的base choice构造。其余的测试通过将base test中某一个特征的test更换为该特征的non-base choice构造。
- 例如:[A, B], [1, 2, 3], [x, y],设base choice test为(A, 1, x),则其余test为
- (B, 1, x)
- (A, 2, x)
- (A, 3, x)
- (A, 1, y)
- 总数:$1 + \sum_{i=1}^Q(B_i - 1)$
- 考虑如下情形,若base choice test均为valid输入,大多数non-base choices为invalid输入,则BCC能较好地构造压力测试
- 例如:[A, B], [1, 2, 3], [x, y],设base choice test为(A, 1, x),则其余test为
- Multiple Base Choice(MBC): 每个特征可以选择一个或多个base choice block。base tests由每个特征的每个base choice构造。之后的测试通过修改base test中的一个特征对应的base choice为non-base choice构造。
- 总数(实际是上界):$M + \sum_{i=1}^Q(M * (B_i - m_i))$
- $M$ 表示总的base tests数量, $m_i$表示特征
i对应的base choice数量
- $M$ 表示总的base tests数量, $m_i$表示特征
- 例如:对
triang()的side1包含两个base choice为“greater than 1”和“equal to 1”。则两个base tests为(2, 2, 2), (1, 2, 2)。根据上面公式即计算$2 + (2 * (4-2)) + (2 * (4-1)) + (2 * (4-1)) = 18$。但是显然有冗余,例如(0, 2, 2)和(-1, 2, 2)。
- 总数(实际是上界):$M + \sum_{i=1}^Q(M * (B_i - m_i))$
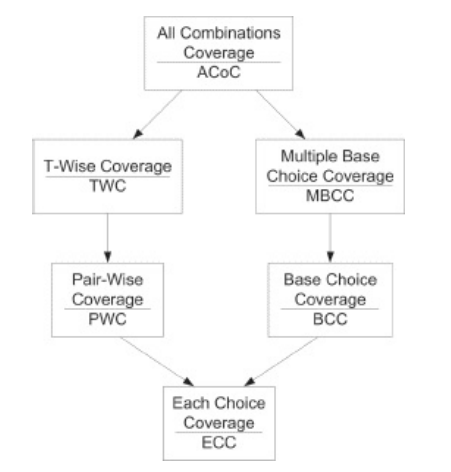
4. 覆盖准则的包含情况