软件测试（三）逻辑覆盖

发表于 | 分类于

盖士人读书，第一要有志，第二要有识，第三要有恒。有志则不甘为下流；有识则知学问无尽，不敢以一得自足，如河伯之观海，如井蛙之窥天，皆无识者也；有恒则断无不成之事。此三者缺一不可。

本文是《Introduction to Software Testing》第八章“Logic Coverage”的笔记和总结。

逻辑测试包括了两种互补的测试方法：

  • 语义逻辑测试
  • 语法逻辑测试

注意：无论哪种覆盖准则逻辑测试的输出就是谓词的求值结果。

1. 语义逻辑覆盖准则

1.1. 术语

  • 谓词（predicate）：求值结果为布尔值的表达式。一个例子是((a>b) ∨ C) ∧ p(x)。谓词能够包括布尔变量、由比较运算符>,<,=,>=,<=,≠连接的非布尔变量以及函数调用。而逻辑运算符包括
    • $\neg$: negative
    • $\vee$: or
    • $\wedge$: and
    • $\rightarrow$: implication 蕴涵
    • $\oplus$: 异或
    • $\leftrightarrow$: 等价
  • 子句（clause）：不包含逻辑运算符的谓词。例如(a = b), C, p(x)

1.2. Simple Logic Expression Coverage Criteria(简单表达式覆盖准则)

根据谓词和子句的取值可以引入各种覆盖准则。设$P$为谓词集合，$C$为$P$中每个谓词的子句集合的并集。

  • 谓词覆盖(Predicate Coverage, PC, 也称为decision coverage)：对每一个$P$中的谓词p，测试需求包含下面两个要求。
    • p求值为true
    • p求值为false
    • 谓词覆盖对应于边覆盖
  • 子句覆盖(Clause Coverage, CC, 也称为condition coverage): 对任意$c \in C$，测试需求包含下面两个要求。
    • c求值为true
    • c求值为false

注: 谓词覆盖和子句覆盖互不能包含对方。例如$p = a\vee b$，满足子句覆盖的的测试{(true,false),(false,true)}不能满足谓词覆盖。同样满足谓词覆盖的测试{(true,false),(false,false)}也不能满足子句覆盖。

  • 组合覆盖(Combinatorial Coverage, COC): 对每一个$P$中的谓词p，测试需求$C_p$中每一个子句包含所有真值表中的组合。
    • 对于一个有n个子句的谓词p，真值表中共有$2^n$种可能。

显然穷尽式的组合覆盖需要进一步简化。

1.3. 主子句覆盖

子句覆盖无法直接控制谓词的结果，为了解决这个问题，定义能够决定谓词取值的单个子句为主子句(major clause)，其它子句为次子句(minor clauses)。具体而言，定义如下：

  • Determination: 设$c_i$为p中的主子句，当给定各个次子句$c_j \in p, j\not ={i}$的值让$c_i$的取值能够改变p的取值时，则称$c_i$决定p。
    • 不说$c_i$和p相同是因为如果$c_i$前若有$\neg$符号，则不相同
    • 例如对$p = a\vee b$，若b为false，则a决定p。

主子句的核心思想是我们希望在子句能够决定谓词的情况下测试各个子句。例如$p = a\vee b$，测试集合T = {TT, FF}同时满足子句和谓词覆盖，但不能保证在b能够决定谓词的情况下是否正确使用。

  • 主子句覆盖(Active Clause Coverage, ACC): 对每个谓词的每个主子句，给定各个次子句的值让主子句能够决定谓词，测试需求包括：
    • 主子句求值为true
    • 主子句求值为false

针对次子句取值是否需要相等，主子句覆盖可以延申出三种变式：

  • General Active Clause Coverage(GACC) 对每个谓词$p$，以及每个主子句$c_i \in C_p$, 选择次子句$c_j$使得$c_i$决定$p$。对每个主子句$c_i$测试需求有两个要求：
    • $c_i$取值为true
    • $c_i$取值为false
    • GACC特点：
      • 次子句$c_j$的取值在$c_i$分别为true和false时不需要相同。
      • 对谓词结果无要求。
    • GACC最大的问题在于无法包含谓词覆盖，例如$p = a \leftrightarrow b$，无论b的取值，a的取值均能决定p的取值，而测试输入{TT, FF}无法满足谓词覆盖。此外$p = a \oplus b$，无论b的取值，a的取值均能决定p的取值，而测试输入{TT, FF}无法满足谓词覆盖。
  • Correlated Active Clause Coverage(CACC) 对每个谓词$p$，以及每个主子句$c_i \in C_p$, 选择次子句$c_j$使得$c_i$决定$p$。测试需求有下面两个要求：
    • $c_i$取值为true和false各一次。
    • 次子句$c_j$的取值必须导致$p$的结果一次为true，另一次为false。
    • CACC中各个次子句的取值可以不一致，但需要主子句的取值让谓词为true和false各一次。
    • 对于$p = a \leftrightarrow b$，测试集合{TT, FT}能够满足a，{TT, TF}能够满足b。因此CAA测试集合为{TT, TF, FT}
  • Restricted Active Clause Coverage(RACC) 对每个谓词$p$，以及每个主子句$c_i \in C_p$, 选择次子句$c_j$使得$c_i$决定$p$。测试需求有两个要求：
    • $c_i$求值为true和false各一次
    • 当$c_i$分别为true和false时次子句的取值必须相同。
    • RACC中各个次子句在主子句分别为true和false时应当相等。

当不同子句间存在依赖关系时，RACC可能会导致不可行测试需求。

1.4. Inactive Clause Coverage

主子句覆盖专注于确保主子句能够确定谓词。Inactive Clause Coverage用于确保主子句在无法确定谓词的情况下确实无法确定谓词。

  • Inactive Clause Coverage (ICC): 对每个谓词$p$，以及每个主子句$c_i \in C_p$, 选择次子句$c_j$使得$c_i$无法决定$p$。测试需求有四个要求：
    • $c_i$为true，$p$为true
    • $c_i$为false，$p$为true
    • $c_i$为true，$p$为false
    • $c_i$为false，$p$为false
    • 即$c_i$的变化不一定引起$p$的变化

对于inactive clause，根据次子句的取值，只有两种变式。此时不需要考虑谓词的值，因为ci本身就无法决定谓词的值，因此无需correlated。

  • General Inactive Clause Coverage (GICC):
    • GICC对子句的取值不做要求。
  • Restricted Inactive Clause Coverage (RICC):
    • RICC要求谓词为true、主子句为true和false时，次子句的取值相同，谓词为false、主子句为true和false时，次子句的取值相同

可以注意到Restricted类型的覆盖要求当谓词的结果确定时，主子句为true和false时次子句取值相等。

1.5. 包含关系

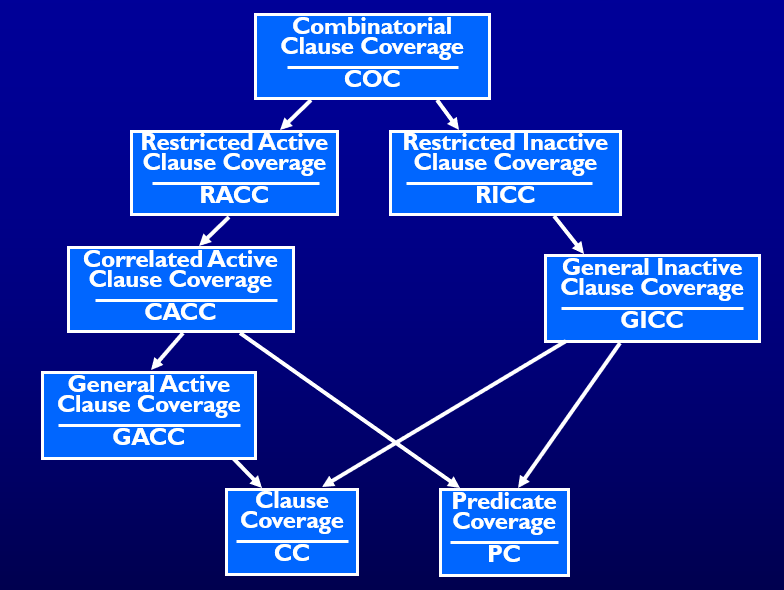
sumption.png

1.6. 让子句决定谓词

本节给出寻找次子句的取值以确保主子句能够决定谓词取值的方法。

\[p_c = p_{c=true} \oplus p_{c=false}\]

如果次子句的取值让$p_c$为true，则c的值能够决定p的值。若次子句的取值让$p_c$为false，则c的值和p的值无关。

证：

  • 充分性证明：若c为主子句$\rightarrow$pc为true
    • 因为c为主子句，则c决定p的值，则$p_{c=true}$和$p_{c=false}$值不同，则异或和为true，则pc为true。
  • 必要性证明：pc为true$\rightarrow$c为主子句
    • 由于pc为true，则$p_{c=true}$和$p_{c=false}$必然一true一false，则显然c的取值能够决定p的值，因为当c的值不同时，p的值不同。

2. 语法逻辑覆盖准则(DNF)

本节考虑测试由析取范式描述的谓词。析取范式即布尔表达式的积之和形式。

2.1. 术语

  • 字（literal）: 一个子句或子句的非
  • 蕴含式（term/implicants）: 由逻辑与连接的字的（literal）集合，为什么叫蕴含式呢，可能因为若蕴含式为真则谓词为真吧
  • DNF谓词：由逻辑或连接的term的集合

例如: $(a \wedge \neg c) \vee (b \wedge \neg c)$包含了

  • 3个子句: a, b, c
  • 3个literals: a, b, $\neg c$
  • 2个terms: $(a \wedge \neg c)$和$(b \wedge \neg c)$

2.2. 蕴含式覆盖（Implicant Coverage）

  • Implicant Coverage (IC): 给定谓词 $f$ 和 $\neg f$，对于$f$和$\neg f$内每一个蕴含式（implicant），测试需求要求implicant为true。

例如，ab+bc'的反为b'+a'c。共有4个implicants

  • ab
  • bc'
  • b'
  • a'c
a b c 满足蕴含式
T T x a b
x T F b c’
x F x b’
F x T a’ c

因此一个测试需求为{TTF, FFT}

2.3. Minimal DNF

和主子句类似，我们希望被测的implicant能起到作用。

  • proper subterm: 由implicant移除1个或多个subterm组成
    • 例如：abc的proper subterms有ab, bc, ac, a, b和c
  • prime implicant：该implicant的proper subterm均非implicant(这句话是想说主蕴含式的子项不能是蕴含式，回忆蕴含的定义，即子项不能独立让谓词取真，否则可以化简）。
    • 例如：f(a, b, c) = abc + abc' + bc'，其中abc和abc'不是prime implicant，因为ab和bc’是implicant（可化简为ab + bc’）
  • redundant implicant: 若implicant能在不改变谓词的值的情况下移除，则称implicant是redundant的。
    • 例如: ab + ac + bc'有三个prime implicant，但是ab是redundant的，因为ac + bc' = ab + ac + bc'
    • 上面这个例子表明了冗余蕴含式可以是主蕴含式。
  • Minimal DNF Representation: 每一个implicant均为prime，且不含redundant implicant。

在求得minimal dnf f的条件下，给出两个定义：

  • 唯真点：unique true point of f with respect to the ith implicant
    • 唯真点需要具体于某个蕴含式而言，注意：一旦唯真点确定，对应蕴含式中的每一个子句的值也就确定
    • 对子句的赋值使得第i个蕴含式为ture，且其它蕴含式为false。
      • 注意: 如果没法让其它蕴含式均为false，则蕴含式是redundant的。
    • 例如：ab + cd，对于ab，TTFF，TTFT，TTTF均为unique true point，但是TTTT不是unique
  • 近假点: near false point for f with respect to clause c in implicant i
    • 近假点需要具体于某个蕴含式的子句而言，注意：一旦近假点确定，对应蕴含式中的每一个子句的值也就确定
    • 对子句的赋值使得f为false，但若子句c取反，蕴含式i和谓词f为true
    • 例如：f为ab + cd，则对ab中的a而言near false point为FTFF, FTFT和FTTF。对ab中的b而言为TFFF，TFFT和TFTF。

注：

  • 真点即谓词值（即测试结果）为真
  • 假点即谓词值（即测试结果）为假

2.4. MUMCUT Coverage Criterion

依赖于DNF形式给出的覆盖准则目的在于解决一些特定类型的错误。下图共给出了DNF形式的9种语法错误。

  • 例如LIF表示在项/蕴含式中错误添加约束的情况。

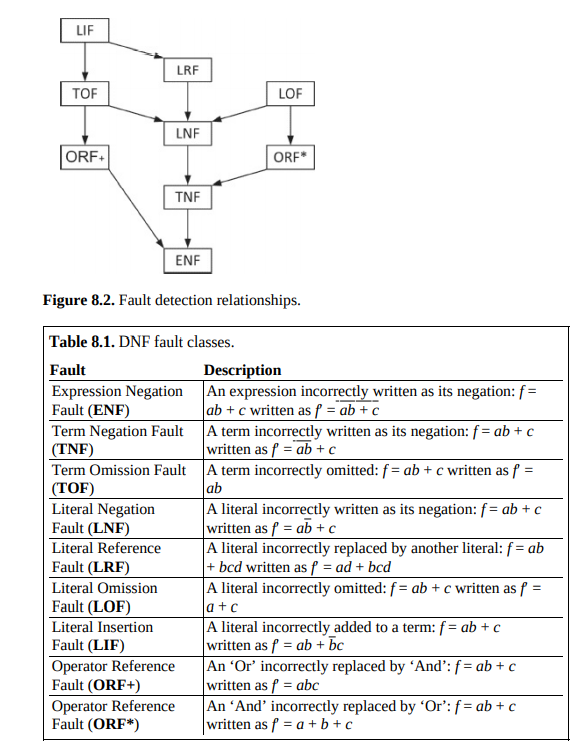dnf-error.png`

  • 多唯真点覆盖（MUTP，Multiple Unique True Points Coverage）:
    • 给定一个最小DNF表示的谓词f，对每一个蕴含式i，选择唯真点（unique true points，UTPs）使得不在i中的其它子句为真和为假各一次。
    • 例如$f = ab + cd$，对于蕴含式ab，唯真点选择可以为TTFT和TTTF，对于cd，唯真点选择可以为TFTT和FTTT。因此$f$的MUTP集合为{TTFT, TTTF, FTTT, TFTT}
    • MUTP能够检测LIF。考虑向一个主蕴含式中插入一个字，因为MUTP要求不在蕴含式中的子句为真为假，因此会导致主蕴含式为假，导致整个谓词为假，因而就能判断出来LIF。
    • MUTP仅检测了真点，对于某些假点无法判断。且如果不同蕴含式存在依赖，则多唯真点也不一定可行。
  • 对应唯真点和近假点覆盖（CUTPNFP，Corresponding Unique True Point and Near False Point Pair Coverage）
    • 给定一个最小DNF表示的谓词f，对每一个蕴含式i中的每一个子句c，测试需求要求i取到唯真点一次且i中的c取到近假点一次，而且这两个点唯一的差别在于c的取值。
      • 注：取到唯真点一次、近假点一次即谓词真假各一次，满足基本的谓词覆盖。
    • 例如，$f = ab + cd$。考虑蕴含式ab中的子句a，ab唯真点可以选择为TTTF, TTFT, TTFF，近假点为FTFF, FTFT, FTTF。因此对aCUTPNFP可以选择{TTFF, FTFF}，对bCUPTNFP可以选择为{TTFF, TFFF}
    • 注：先找出唯真点，然后对子句翻转选择近假点。
  • 多近假点覆盖（MNFP，Multiple Near False Point Coverage）
    • 给定一个最小DNF表示的谓词f，对于每一个蕴含式i中的每一个字c，测试需求要求选择近假点使得不在i中的子句为T和F各一次。
    • 例如，$f = ab + cd$。对于蕴含式ab，考虑字a。若近假点选择FTFT, FTTF，则不在ab中的子句c、d能够取到T和F各一次。对于cd中的c，如果选择TFFT, FTFT，则a、b能够取到T和F各一次。
  • MUMCUT
    • 给定一个最小DNF表示的谓词f，对f应用MUTP，CUTPNFP和MNFP。

2.5. 卡诺图

n个子句，共有$2^n$种蕴含式，每种组合取或不取共有$2^{2^n}$种谓词。

KN图的一些作用：

  • minimal蕴含式: 对应2的幂次格子的圈出的长方形
    • 判断非主蕴含式
      • 存在更大的长方形能完全包含当前蕴含式的长方形
    • 判断冗余蕴含式
      • 当前蕴含式长方形包含的格子均被其它蕴含式长方形包括过了
  • 找唯真点: 唯真点针对单个蕴含式而言，因此是仅被单个蕴含式长方形包含的单个格子
    • 应用: MUTP
      • 选择其它子句能取到T和F的唯真点格子
  • 找近假点: 近假点即和真点格子相邻的假点格子 -> 由于相邻，所以只需反转一个子句就能取真
    • 应用: CUTPNFP
      • 选择和唯真点相邻的近假点格子组队
    • 应用: NFP
      • 对每一个蕴含式确定字的近假点，保证其它子句为T和F

3. 源代码的逻辑覆盖

  • 源代码中的谓词直接从判断语句中获取
    • if语句
    • switch语句
    • for, while语句
  • 对源代码应用逻辑准则的难点主要在reachability和controllability
    • reachability: 在对某条语句应用谓词前首先应当到达该语句，当程序规模非常大的时候，满足可达性会变得非常复杂
    • controllability: 或者称为内部变量问题，即测试人员必须找到输入值并间接对谓词中的变量进行赋值
      • 内部变量：在谓词中但不是输入变量的变量

上述复杂性导致了程序级别的逻辑覆盖准则通常被限制在单元和模块测试中。（苦笑.jpg，覆盖准则整了一大堆，实用性几乎为0）

生成测试用例的主要步骤：

  1. 提取被测代码中的条件语句
  2. 分析每一个条件的可达约束
  3. 分析可达约束中出现的内部变量并求解（将内部变量使用输入变量替代）
  4. 根据内部变量的求解结果求解可达约束条件（将内部变量相关的谓词使用上述求解结果替代）
  5. 根据覆盖准则求解测试用例

3.1. 示例

下面通过一个例子进行分析：

thermostat.png

首先，简化谓词表达式，28-30行的谓词中有四个子句，可以通过下面的方式简化

thermostat1.png

turnHeaterOn()方法有一个输入参数pSet。它还用到了能够用setter方法配置的实例变量。此外还有一个dTemp内部变量决定了渴望的温度，该变量通过日期周期和日期类型从pSet中获取。

使用覆盖准则之前，首先要解决可达性问题和内部变量问题。

3.1.1. 可达性问题的解决

这个问题可以通过绘制流程图解决，结果可以归纳为：

  • 28-30行：可达性为true
  • 34行：(a || (b && c)) && d
  • 40行：!((a || (b && c)) && d)

注意到a是curTemp < dTemp - thresholdDiff的简化，其使用了内部变量dTemp。因此我们需要间接控制它的值。

3.1.2. dTemp内部变量问题的解决

26行使用period和day获取programmedSettings对象。

  • 一种简单的解决方案是：用直接的赋值取代方法调用，这种方案有两个不利之处
    • 我们必须在运行每个测试前重新编译Thermostat
    • 这种方法实际上测的不是部署时的方法
  • 另一种方法是：了解如何设置程序状态使得对turnHeaterOn的调用会返回渴望的值
    • 在本例中，需要在测试调用turnHeaterOn()方法前对该对象进行设置。每次可以通过设置固定一个取值。

3.1.3. 覆盖的测试用例生成

之后的测试用例生成阶段相对简单。就是根据覆盖准则对各个谓词的子句取值进行设计。

4. Specification的逻辑覆盖

  • 规范通常有两种
    • 形式化规范：通过数学形式描述，这种形式会直接使用逻辑表达式因此很容易应用覆盖准则（really？）
    • 非形式化规范：通过自然语言描述，需要使用明确的逻辑表达式对其进行重写

这里重点关注前置条件。

4.1. 前置条件的逻辑准则覆盖

  • 前置条件通常在注释中通过requires或是pre引出，例如
1
2
3
4
// @requires
// name must not be empty
// state must be valid
// zip must be 5 numeric digits

重写为name != "" ^ state in stateList ^ zip >= 00000 ^ zip <= 99999

注意到这种写法即单子句组成的合取范式。

观察真值表可以发现

  A B C …
1 T T T …
2 F T T …
3 T F T …
4 T T F …
  • 主子句在其它子句均为true的情况下能够决定谓词
  • ACC测试即：
    1. 所有子句均为true的行
    2. 单个子句为false，其它为true且构成对角线的行

对单子句组成的析取范式的写法如

  • (A ^ B) V (C ^ D)
  • ACC测试即
    1. 所有子句均为false的行
    2. 单个子句为true，其它为false且构成对角线的行

5. FSM的逻辑覆盖

对于有限状态机

  • 节点表示状态
  • 边代表了节点间的转移
    • 边通常包含了作为触发条件的guard

因此可以将边转移条件简化为谓词表达式然后进行测试。

  • 测试的预期输出：下一个状态
    • 若谓词需要为true，则需要到达下一个状态
    • 若谓词需要为false，则需要为其它的状态
  • 可达性：测试必须到达转移边所在的前一个状态
  • 退出：一些测试必须继续执行直到结束状态