词法分析

发表于 | 分类于

1. 术语

1.1. Alphabet

Def: A finite set of symbols.

1.2. String

Def: Finite sequence of symbols on an alphabet. ε is the empty string.

1.3. Language

Def: sets of strings over some fixed alphabet.

e.x. {ε} the set containing empty string is a language.

1.4. Regular Expression

Def: A regular expression is a set of rules for constructing sequences of symbols from an alphabet.

let $\sum$ be an Alphabet, r a regular expression. Then L(r) is the Language characterized by the rules of r.

1.5. regular definitions

Def: A regular definition is a sequence of the definitions of the form $d_1 \to r_1$, $d_2 \to r_2$, …, $d_n \to r_n$, where $d_i$ is a distinct name and $r_i$ is a regular expression over symbols in $\sum$∪$\{d_1, d_2, …, d_{i-1}\}$

2. 总论

词法分析生成器主要经历下列步骤：

  1. 给出语言的形式化正则定义。
  2. 根据正则定义中的正则表达式生成NFA。
  3. 根据NFA生成DFA。
  4. 通过DFA处理输入字节流。

3. 形式化正则表达式记法

正则表达式用于描述构造在某字母表之上的由其内某些字符组成的合法字符串集合，同时扩增使用ε表示空字符串。一个正则表达式由三个操作构成

  1. Alternation：两个字符串集合的并，记为$R\|S$。
  2. Concatenation：两个字符串集合的关联，记为$RS$。
  3. Closure：某个字符串集合相对于其本身的0次或多次关联，记为$R^*$。

一些补充记号如下

  • $R^{+}=RR^{*}$: one or more.
  • $R?=R\|ε$: zero or one.
  • $[range]$: set range of characters, $[A-Z]=A\|B\|C\|…\|Z$.
  • $[\^ab]$: anything but.

例如，

正则表达式 表示的语言
ε {ε}
a ∈ $\sum$ {a}
r* (L(r))*
0* {ε, 0, 00, 000, …}
$(0|1)*$ all strings with 0 and 1, inclusing the empty string

4. 汤普森构造法

汤普森构造法能够确保最终的NFA含有1个final状态，1个start状态。

汤普森构造法针对正则表达式每种操作生成NFA的方式如下

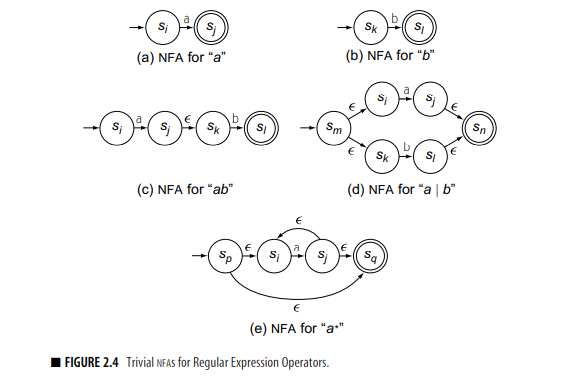
thompson.png

4.1. 构造法生成NFA的性质

设正则表达式r，对应的NFA为N(r)，则

  1. N(r)的状态数$# of states <= 2*{#symbols + #operators}$，即不超过所有符号和操作符的两倍。
  2. N(r)具有1个起始状态和1个终止状态。
  3. ε-transition总是连接上一步的终止状态和某一部分的起始状态。
  4. 每一个状态最多有两个进入ε-moves和两个离开ε-moves。对于alphabet中的任一符号，最多一个进入move和一个退出move。

5. NFA转DFA: 子集构造算法

设r为正则表达式的长度

  NFA DFA
空间要求 O(r) O($2^r$)
时间要求 O(r*x) O(x)
  • DFA中的任意状态均可能/可能不包含NFA中的任意状态
  • NFA状态小于等于两倍符号和操作符数目之和
  • NFA遍历同时需要维护当前可能处于的状态
  • DFA遍历时是确定的，每个符号依次状态转换

为了将NFA转换成DFA，需要做到：

  1. 消除ε转换：ε闭包应当属于单个状态
  2. 一个状态在一个输入字符的情况下，只能具有一个转移

5.1. 计算ε闭包

这个比较简单，对所有状态通过ε可达的其它状态以及其本身就构成了ε闭包。

5.2. 生成DFA集合

1
2
3
4
5
6
7
8
9
10
11
add ε-closure({s0}) as unmarked state into DFA-sets
while (DFA-sets have unmarked set S) {
    mark S
    for each input symbol a {
        S' = ε-closure(move(S, a));
        if S' not in DFA-sets {
            add S' as unmarked state into DFA-sets;
        }
        transfunc[S, a] = S'
    }
}

首先s0的ε闭包构成了S0，然后对S0可接受的所有输入字符，生成新的状态。直到无法生成新的状态。

5.3. DFA状态最小化

画出DFA状态转移表后，对于那些在任意相同输入下产生相同输出的状态进行合并。

6. 正则表达式直接转DFA

正则表达式其实也可以直接转换为DFA，步骤如下

  1. 增强给定的正则表达式：对正则表达式r，在其末尾增加特殊符号#，即r#。
  2. 给每个符号(包括#符号)指定位置序号。
  3. 对每个位置计算followpos。
  4. 以firstpos(root)作为状态S0，其内包含的符号表示下一个可以接受的输入符号。以这些输入符号依次作为输入，分别生成其它状态，直到无法生成新的状态。

一个示例如下:

re-to-dfa.png

7. 参考

  • engineering a compiler