CSAPP 第五章优化程序性能（一）基础优化与依赖机器架构的优化

Don’t design bridges in ignorance of materials, and don’t design low-level software in ignorance of the underlying hardware.

写程序的首要目标是要使它在所有可能的情况下都正确工作。其次，我们需要考虑程序的可读性问题。在以上两者都能满足的情况下，我们就可以考虑程序的性能问题了。

编写高效程序需要做到下面几项:

使用合适的数据结构和算法。
编写编译器能够有效优化的源代码。
针对运算量很大的计算，利用并行性，将任务分成多个部分，让它们在多核和多处理器的某种组合上运行。

本章主要介绍第二项。具体而言:

消除不必要的工作，例如: 不必要的函数调用、内存引用、条件测试。这些工作通常不依赖于执行环境的操作，有些也可以被编译器优化。
利用处理器提供的指令级并行能力，同时执行多条指令。
使用profiler，确定程序中的关键路径并加以优化。

1. 性能参数: Cycles per Element, CPE

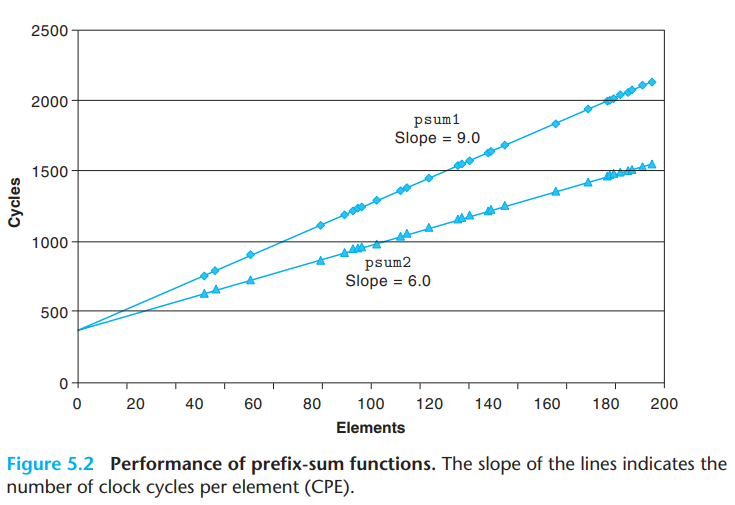
CPE: 计算/处理单个元素所需要的时钟周期，CPE值越小越好。当过程在一组元素上迭代时，该过程执行的时钟周期数和被处理的元素个数能够用一个线性函数来描述，这个线性函数的斜率就是CPE。

下图通过最小二乘法拟合获得的线性函数描绘了使用两种方式计算前缀和时，已处理元素数和时钟周期的关系，CPE较小的一种使用了循环展开技术。

\[T = CPE * n + Overhead\]

2. 基础优化

之后的优化基于对下面这个函数的分析:

此时，对应的CPE结果为:

2.1. 代码移动

code motion: 避免执行多次但是计算结果不变的操作，改用局部变量保存计算结果。
注意: 某些code motion优化是编译器能够发现的。

具体而言，在循环判断语句中要避免每次都重复计算数组长度

注意到此时性能获得了提升。

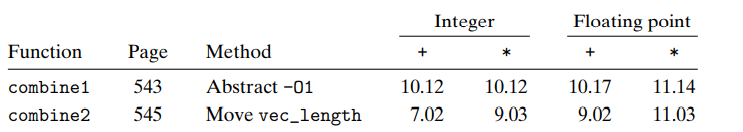
2.2. 减少过程调用

注意到循环体内每次获取向量元素都要调用get_vec_element函数，考虑打破抽象，直接通过数组指针遍历。

然而结果性能没有显著增加，整数加法反而有所减小

这说明过程调用的开销并非性能瓶颈。

2.3. 消除不必要的内存引用

通过分析上述汇编代码注意到循环体内每次从dest处读取值，同时也要写入dest处。考虑使用局部变量保存中间结果能够简化为:

对应的

注意到相比减少内存调用的版本性能有了显著地提升，如下

2.4. 其它优化

2.4.1. reduction in strength

使用开销较小的操作替代开销较大的操作。

例如，使用x << 4替代16 * x

Intel Nehalem: 整数乘法操作需要消耗3个CPU时钟周期，加法操作需要消耗1个CPU时钟周期。

重用部分表达式，避免重复计算。例如下面通过单个局部变量的计算，减少了3次冗余计算。

// version 1
up = val[(i-1)*n + j];
down = val[(i+1)*n + j];
left = val[i*n + j-1];
right = val[i*n + j+1];
// version 2
long inj = i*n + j;
up = val [inj - n];
down = val[inj + n];
left = val[inj - 1];
right = val[inj + 1];

GCC的O1优化会优化这一点

3. 编译器的局限性

编译器的优化行为需要满足一条基本的约束: “优化后的代码的行为和优化前的代码的行为相同”。

大多数编译器分析局限在单个函数内
- 基于整个程序的分析开销过于昂贵
- 新的GCC能够进行单个文件内部的过程间的分析
大多数分析基于静态信息

3.1. 优化障碍1: procedure call

void lower(char *s)
{
    size_t i;
    for (i = 0; i < strlen(s); i++)
        if (s[i] >= 'A' && s[i] <= 'Z)
            s[i] -= ('A' - 'a'); 
}

注意到由于循环判断中调用了strlen，因此时间复杂度是O(n^2)

然而编译器无法对这种情况进行优化。

函数调用可能有side effects
- 函数内部可能了修改全局状态，如果优化掉则会出问题
对于给定参数，函数不一定会返回相同的值
- 取决于某些全局状态

因此编译器通常将过程调用视为黑盒，仅使用弱优化。

解决

使用内联函数
编程者自己进行代码移动(code motion)

3.2. 优化障碍2: memory aliasing

// 版本1: 2次读*xp，2次写*xp，两次读*yp
void twiddle1(long *xp, long *yp) {
    *xp += *yp;
    *xp += *yp;
}
// 版本2: 1次读*xp，1次读*yp，一次写*xp
void twiddle2(long *xp, long *yp) {
    *xp += 2 * *yp;
}

上述两个版本实际上并非等价，若xp和yp指向同一处内存位置，则结果不同。

void sum_rows1(double *a, double *b, long n)
{
    long i, j;
    for (i = 0; i < n; i++) {
        b[i] = 0;
        for (j = 0; j < n; j++)
            b[i] += a[i*n + j];
    }
}

上述代码的内循环汇编如下

.L4:
    movsd (%rsi, %rax, 8), %xmm0 // 装载b[i]
    addsd (%rdi), %xmm0
    movsd %xmm0, (%rsi, %rax, 8) // 存储b[i]

这里编译器也没有进行优化，因为

b可能是a的一部分，此时每次迭代对b的修改会改变a。因此编译器无法优化内存引用次数。

解决

在内循环中使用本地变量进行accumulate以消除aliasing
通过声明为double *restrict a，告知编译器指针参数无法重叠

4. 现代处理器的硬件结构

到目前为止介绍的优化不依赖于目标机器的特性，这些优化减少了一部分开销，也消除了阻碍编译器优化的障碍。

接下来为了更进一步的优化，需要理解处理器微体系架构的实现。

现代处理器在同一时刻对多条指令求值，同时保证这种并行执行具有和顺序执行相同的效果。这种技术被称为指令级并行。

性能约束

两种 以CPE为单位（周期每元素） 的延迟界限描述了程序的最大性能。

当一系列操作必须顺序执行时（例如指令间存在数据依赖），可能会遇到延迟界限（latency bound）导致性能下降。
由于处理器功能单元有限，因此还存在吞吐量界限（throughput bound）。该界限是受功能单元数量物理限制的最小CPE界限。

4.1. 整体结构: 乱序 + 超标量

现代处理器一般是乱序且是超标量的。

超标量: 通过实现多个硬件单元，可以在每个时钟周期执行多个操作
乱序: 指令执行的顺序和二进制代码中的顺序不一定相同

架构如下图所示

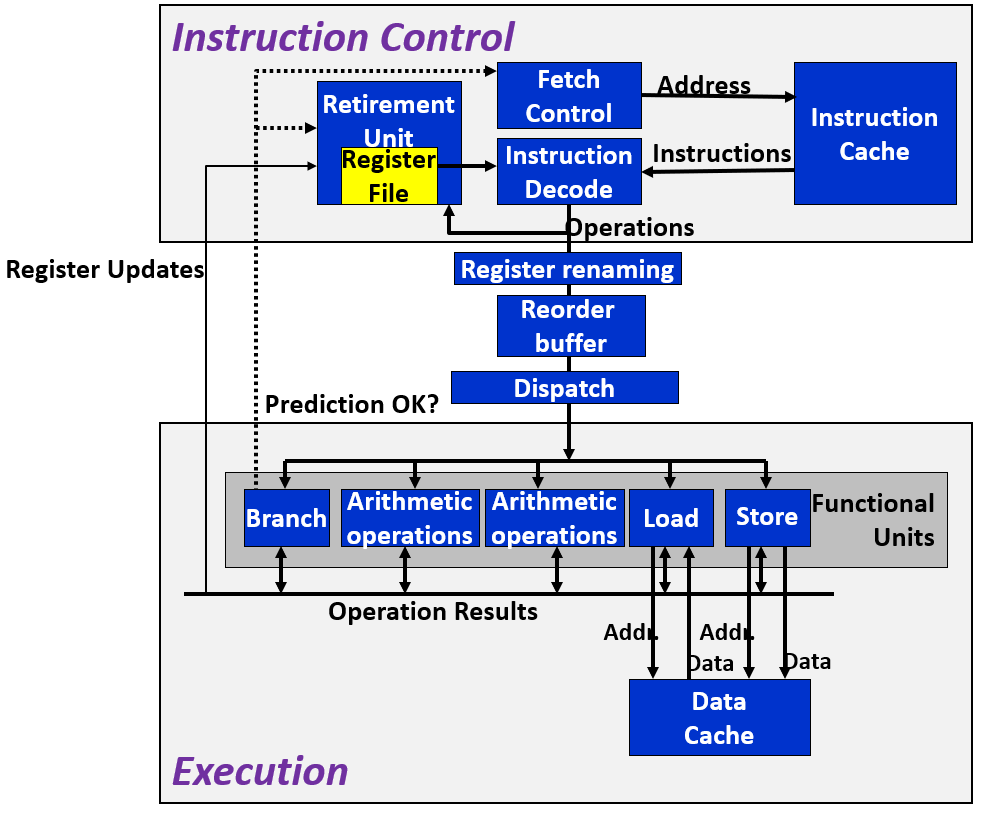
注意到，这种架构包含了两个单元

指令控制单元(ICU, Instruction Control Unit):
- Fetch control: 包含分支预测的功能
- Instruction decode: 从icache中读取指令，然后翻译为一组微操作(x86)。例如，addq %rax, %rdx转换为单个微操作；addq%rax, 8(%rdx)转换为内存读取、加法和内存写入三个微操作。
- Retirement Unit: 退役单元控制寄存器文件，记录正在进行的处理并确保遵守顺序语义。指令译码时，和指令相关的信息入队，并一直保存在队列中，直到
  1. 一条指令操作完成，且引起该指令运行的分支点也被认为预测正确，则该指令退役，对应的执行结果会更新寄存器
  2. 若某个分支点预测错误，则该指令会被flush，执行结果被丢弃
执行单元(EU, Execution Unit): 接收来自ICU的微操作，分发到各个功能单元执行，每个时钟周期一般有多个操作。
- Load和Store单元: 包含一个加法器计算地址，和dcache交互
- Branch单元: 预测会执行的指令执行结果会保存在EU内的队列中，若Branch单元计算发现预测错误，则会丢弃保存的执行结果，并通知Fetch Control单元，之后才能获取正确的指令
- 其它各种功能单元: 通常一个算术运算单元能够执行多种运算，例如: 整数运算、浮点乘、整数乘、分支等等

注意: 为了避免分支预测错误，任何对程序寄存器的更新都只会在指令退役时发生。

为了加快传送某个单元操作结果到另一个单元的速度，执行单元之间也可以进行数据交换。一个常用技术被称为寄存器重命名。

当某个写寄存器r的操作译码时，会生成一个(r, t)条目加入一张表中
之后的以r作为操作数的指令译码时，会将t给到执行单元作为操作数
当写操作完成得到结果v时，它会更新条目为(v, t)。之后所有等待t结果的操作都可以查表并使用v了。

通过这种机制，就不需要先写入寄存器文件（隐含着需要分支判断正确，指令退役），之后再读出来。只要操作执行完成，无论预测失败与否，操作结果都可以转发并继续后续操作。注意: 该表只需维护写操作对应的寄存器，对于读操作，可以直接从寄存器文件获取这个操作数。

4.2. 功能单元的性能

Intel Core i7 Haswell CPU有下面8个功能单元:

整数运算，浮点乘法，整数和浮点除法，分支
整数运算，浮点加法，整数乘，浮点乘
load，地址计算
load，地址计算
store
整数运算
整数运算，分支
store、store地址计算

它们的性能参数分别如下

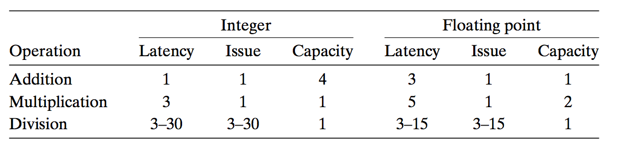
latency: 完成运算需要的总时间
issue: 两个连续同类型的运算的最小发射间隔时钟周期数
capacity: 能够执行该功能单元的数量

从以上性能参数我们能够分析得到下面这些结论

乘法和加法的issue时间均为1，然而单个乘法操作以及浮点加法操作的latency均大于1，这是利用了流水线技术。issue时间为1的功能单元被称为完全流水线化（fully pipelined）。例如，浮点浮点加法的三个流水线级分别为处理指数，小数相加，结果舍入。
除法的latency和issue时间相同。这意味着每开始一次除法操作都需要首先完成上一次的除法操作。

功能单元的最大吞吐量: 对一个容量为C，发射时间为I的功能单元，它的最大吞吐量为$C/I$。

对于不同的功能单元而言，它们的两个CPE界限（即单位是周期每元素）: 延迟界限（必须顺序执行时的CPE值）和吞吐量界限分别为:

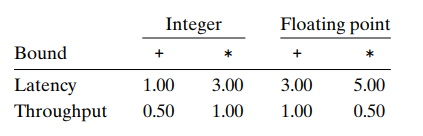
由于有4个加法硬件，本来每个周期能够处理4个加法操作即吞吐量为0.25周期/操作，但是因为只有两个load单元，因此每个周期只能load两个数，即吞吐量为0.5周期/操作。

注意: 延迟界限和吞吐量界限给出的都是下界。

4.3. 处理器操作分析模型

经历过内存引用消除后的代码CPE值和界限之间的比较如下:

注意到除了整数加法操作，其它操作的CPE值和延迟界限相同。事实上，此时整数加法中的数据相关构成了程序的关键路径。

可以通过数据流图研究这种相关性。对于内循环的汇编代码

 .L25:
  vmulsd (%rdx), %xmm0, %xmm0   # multiply acc by data[i]
  addq   $8, %rdx               # increment data+i
  cmpq   %rax, %rdx             # %rdx - %rax
  jne    .L25

可以画出如下的数据流图

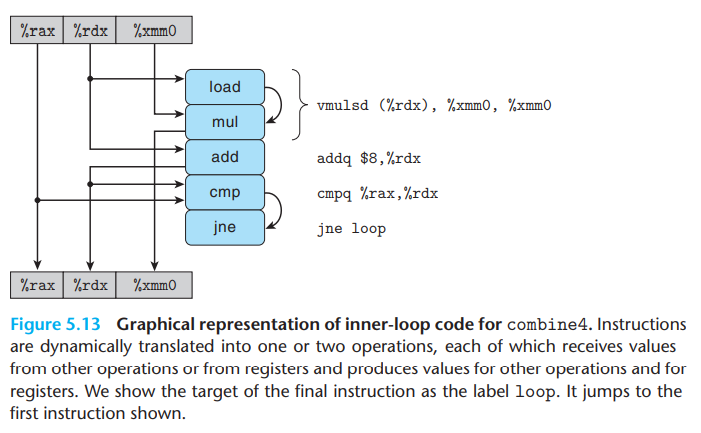
注意到vmulsd指令被翻译成两个操作: load和mul。

循环中使用的寄存器能够被分成四类:

只读
只写
局部: 在单词循环内部被修改和使用的寄存器，迭代和迭代之间不相关，例如上面的条件码寄存器。
循环: 在循环中既作为源值又作为目的值的寄存器，即再一次迭代中产生的值会在另一次迭代中用到。例如上面的%xmm0和%rdx寄存器。

接下来可以看到，循环寄存器之间的操作链决定了限制性能的数据相关。

进一步对数据流图进行优化，消除不直接影响数据流的操作（即cmp和jne）以及循环寄存器后有

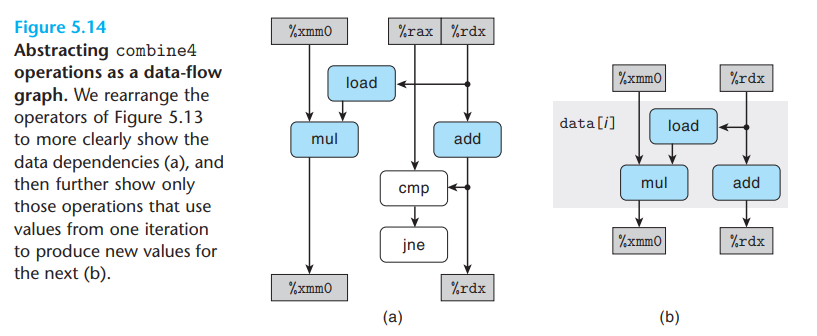
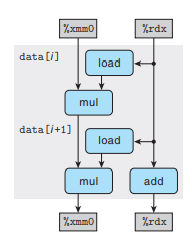
上图右侧的数据流表示的是单次迭代中进行的操作。当绘制多次迭代可以注意到

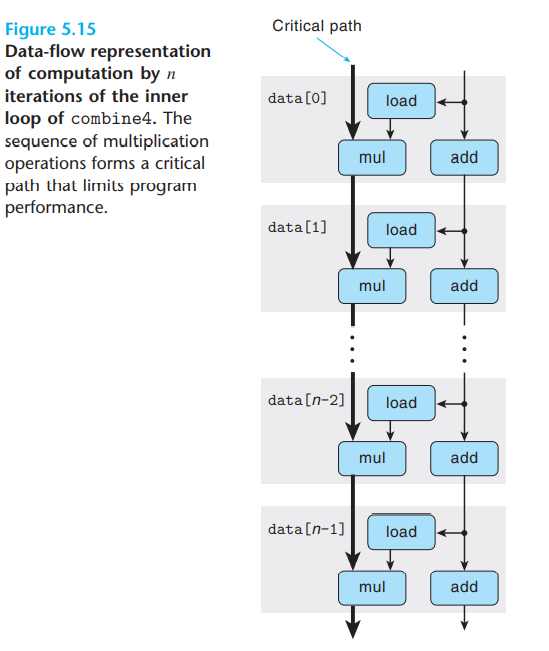
注意到程序存在两条数据相关链:

mul操作对%xmm0的修改
add操作对%rdx的修改

在单精度浮点乘法条件下，由于mul操作的执行需要5个时钟周期，而数据依赖的情况下迭代n次就需要5n个时钟周期。加法操作需要1个时钟周期，因此n次迭代整体仅需要n个时钟周期。所以关键路径为mul操作的数据依赖。

上述分析能够说明之前单精度浮点乘法CPE为什么是5。虽然data+i和load操作能够并行执行，但是只有在上一个乘法操作计算完成之后，才能继续。至于整数加法为什么是1.27，需要进一步获取未公开的硬件相关的资料。

接下来我们希望提高重新调整操作的结构，增强指令级并行。具体而言，我们需要对程序做变换，使得唯一的限制因素是吞吐量界限。

5. 程序变换: 循环展开（loop unrolling）

循环展开: 通过增加一次迭代内的处理元素数，减少迭代次数。

减少循环开销: 减少不直接有助于得到程序结果的操作的数量，如条件判断
缩短关键路径: 提供了减少关键路径上操作数量的方法

通过2x1循环展开后的代码为

对应获得的性能为

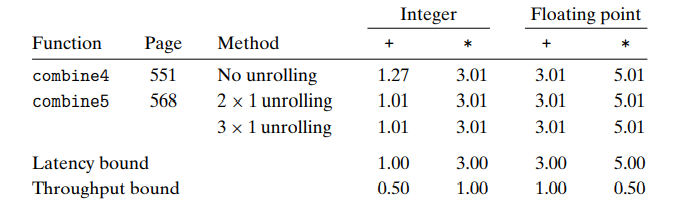
注意到仍没有超过延迟界限，这是因为关键路径上仍有n个mul操作，仅是将循环开销减少了一半。

6. 提高并行性

注意到，虽然程序性能受到运算单元的延迟限制，但是加法和乘法运算单元能够完全流水线化，然而循环展开并不能利用这种能力。本质原因在于我们使用单个累计变量，仅在该变量上一个值计算完成后，才能累积计算下一个值。

6.1. 程序变换: 多个累积变量

对于一个可交换且可结合的合并运算，我们可以将一组合并运算分割成两个或多个部分，并在最后合并结果以提高性能。

例如使用2x2循环展开的代码如下

此时可以做到两路并行乘法操作。对应的性能结果为

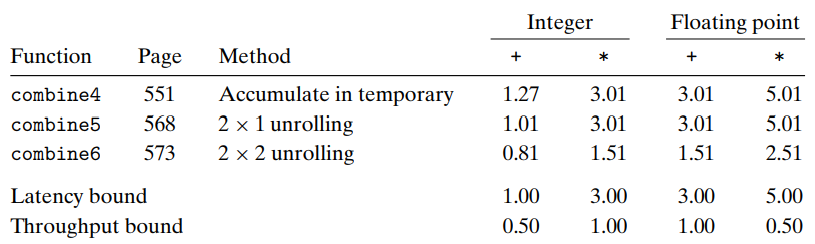
注意到几乎所有操作都改进了大约一倍。

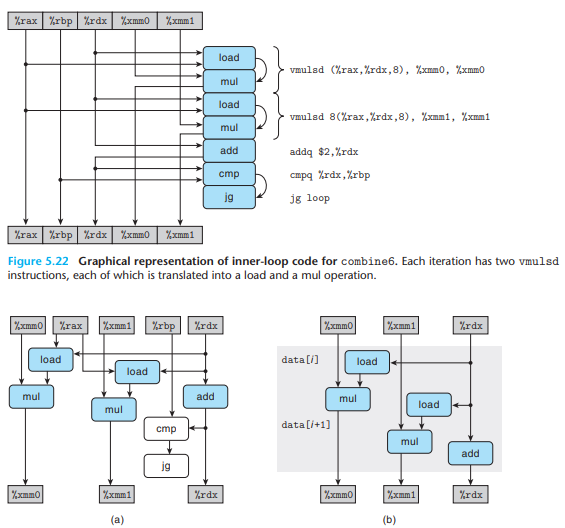
由于每个关键路径只包括1/2个mul操作，因此CPE值减小为原来的1/2。

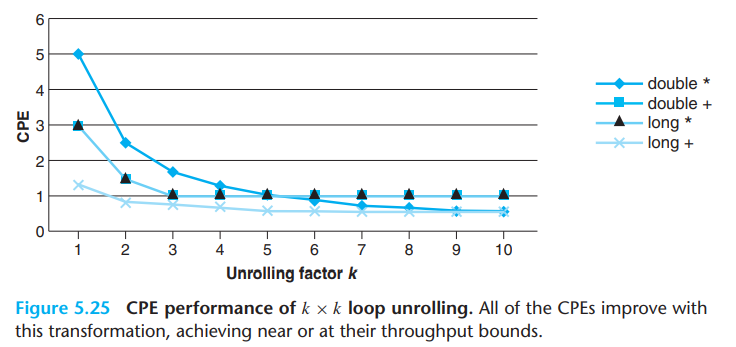
考虑上述累计变量变换的一般形式，将循环展开为k次，同时并行使用k个循环变量。注意到当k=10时，几乎能达到吞吐量界限。这是因为为了达到吞吐量界限，通常需要所有流水线都是满的，对延迟为L，容量为C的操作而言，就需要循环展开因子k >= L*C。

例如，浮点乘的L=5，C=2，则k需要大于等于10。而浮点加有L=3，C=1，因此k大于等于3就可以达到最大吞吐量。

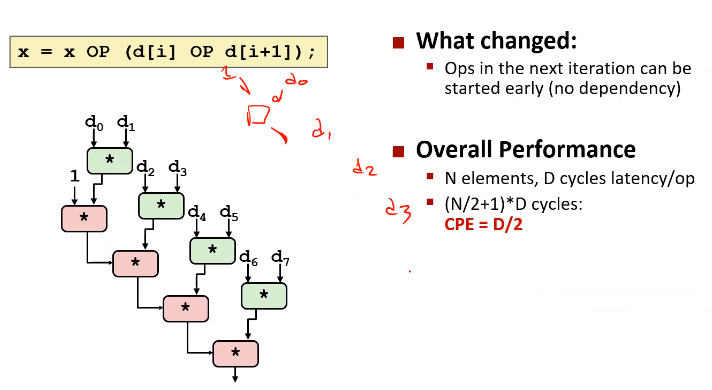
6.2. 程序变换: 重新结合变换（reassociation transformation）

重新结合变换: 变换累积变量和向量元素的合并顺序。

上面的变换被称为2x1a unrolling。步长为2，单个累积变量。

通过变换合并顺序，关键路径也减小了一半。

相对应的性能参数变化为

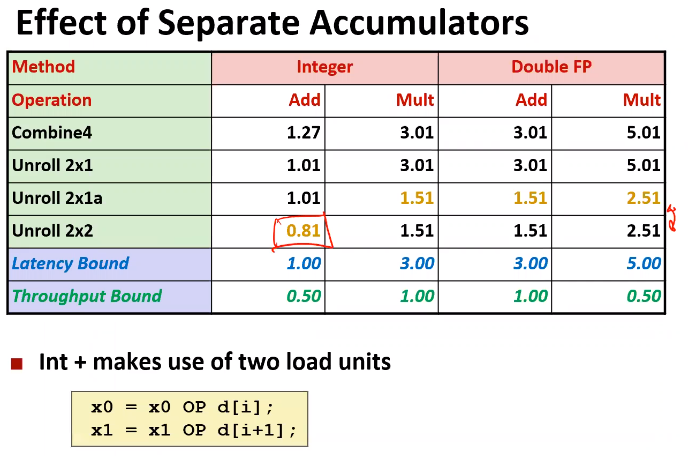
注意到和2x2 loop unrolling相比，2x1a计算的CPE大致相同，但是2x2 loop unrolling能够并行利用两个load单元。

注: 由于浮点计算的不可结合性，编译器通常不会使用这些方式对浮点运算进行优化。

6.3. 使用SIMD指令

通过使用AVX指令，可以进一步提高并行性。

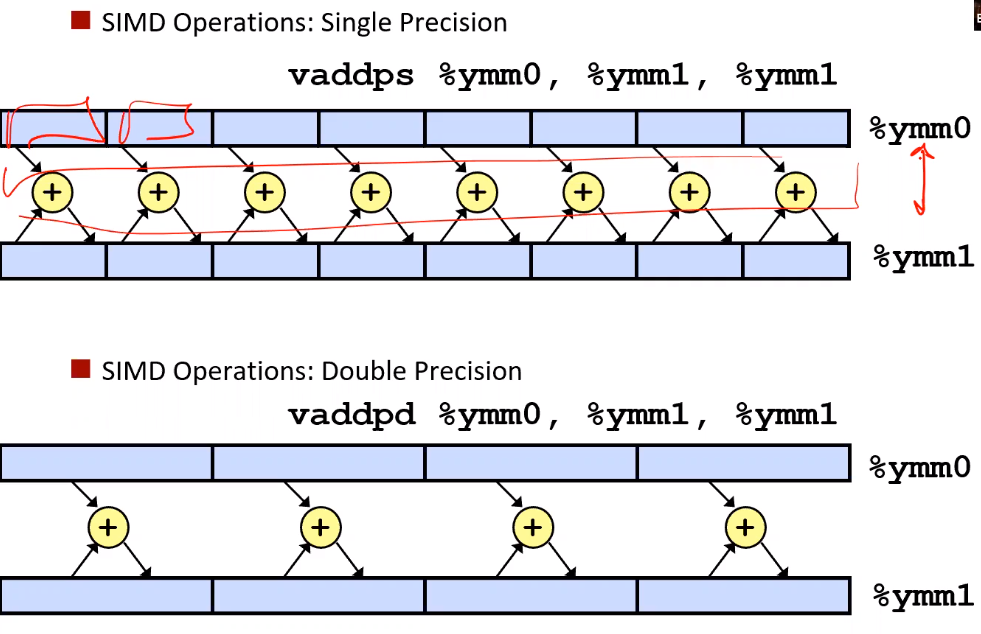
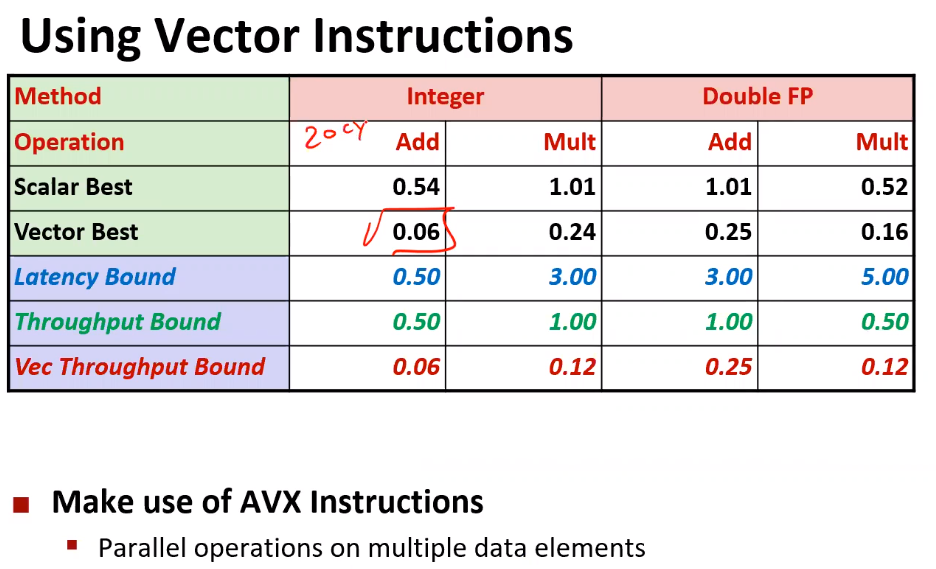
6.3. 小结

注意到，功能单元的吞吐量界限是一个极限下界。假设程序要执行n个操作，而硬件共有c个功能单元，且每个单元的发射时间为i，则程序至少需要$\frac{n}{c} * i$个时钟周期。

7. 性能优化的限制因素

寄存器溢出
- 循环并行性受汇编代码（通用寄存器资源）描述计算能力的限制。因此循环展开无法做到无限扩展，事实上之前的例子当从10x10扩展到20x20时，由于寄存器溢出，程序变量值会被存储在栈中，因而导致性能下降。
分支预测与预测惩罚
- 原则1: 不要过分关心可预测的分支。
  - 之前的示例中将每次迭代的元素获取从get_vec_element()中拿出来，然而性能基本没有变化，这说明分支在高度可预测的情况下，边界检查几乎不会影响性能。
  - 注意: 这里说的是可预测的分支！！！对于难以预测的分支，性能还是会有大的变化。
  - 分支预测失败，有大约20个周期的惩罚。
- 原则2: 书写适合用条件传送实现的代码。
  - 使用条件传送替换传统的基于分支跳转的实现: 计算分支两个方向上的值，然后根据条件使用某一个方向上的值。

GCC倾向于将如下函数式风格的代码转化为使用条件传送指令，该风格倾向于用条件操作来计算值，然后用值更新程序状态。相反，命令式风格倾向于根据条件语句有选择地更新程序状态。一个例子如下:

命令式

函数式