在计算机科学中只有两件难事:缓存失效和命名。
1. 局部性原理
- 时间局部性: 程序倾向于引用最近引用过的数据。
- 空间局部性: 程序倾向于引用最近引用过的数据附近的数据。
量化评价局部性的一些原则:
- 重复引用相同变量的程序有良好的时间局部性。
- 对数组以步长为k的模式进行引用时,k越小,空间局部性越好。
- 对取指令而言,循环有好的时间和空间局部性,循环体越小,循环迭代次数越多,局部性越好。
2. 存储器层次结构
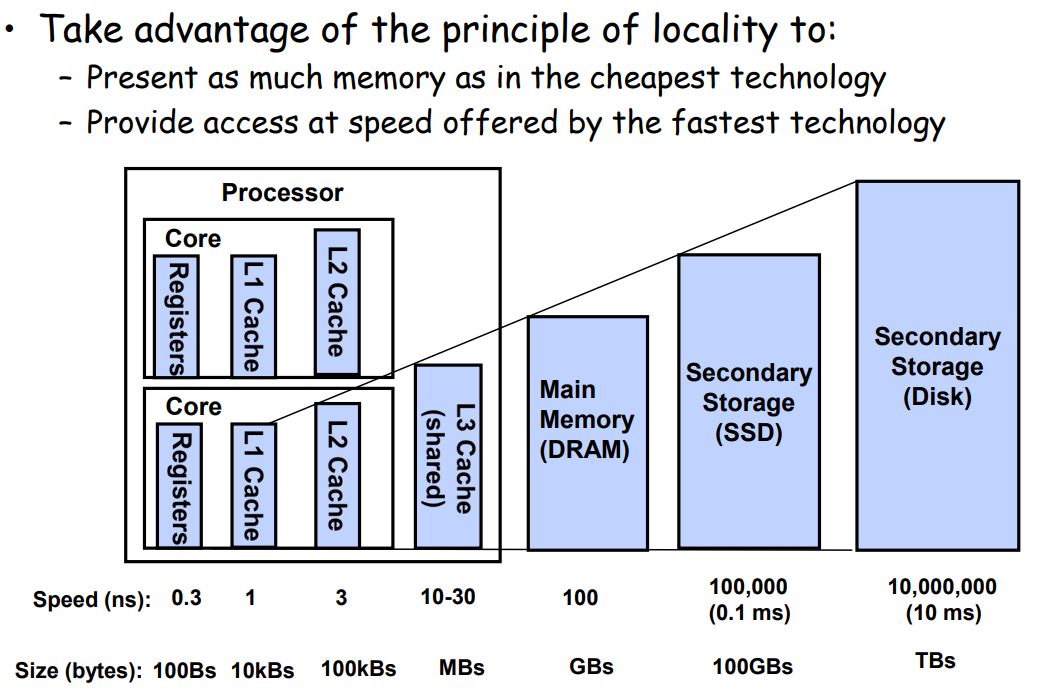
利用局部性原理组织存储器结构以期能够
- 提供和最低成本存储相同数量级大小的空间
- 提供和最高成本存储相同数量级大小的访问速度
基本思想: 第k层存储作为第k+1层存储的缓存。相邻两层之间使用固定的块大小作为传输单元。
- 缓存命中
- 缓存未命中: 需要从k+1层取出对应的块
- 第k层未满
- 第k层已经满了: replace/evict a victim block
- 缓存未命中的种类
- Cold (compulsory) miss: 对数据第一次引用时,缓存为空,一定会不命中
- Capacity miss: 工作集(working set)比第k层缓存大
- Conflict miss: 第k层缓存的空间足够放下工作集但是多个数据被映射到第k层的同一个地址块上
- 缓存管理
- 在每一层上,某种形式的逻辑需要管理内存,或是软件或是硬件
- L1, L2, L3缓存: 硬件逻辑
- DRAM: 作为对磁盘上数据块的缓存,操作系统软件和地址翻译硬件共同管理
- AFS: 本地磁盘是缓存,由本地机器上的AFS客户端管理

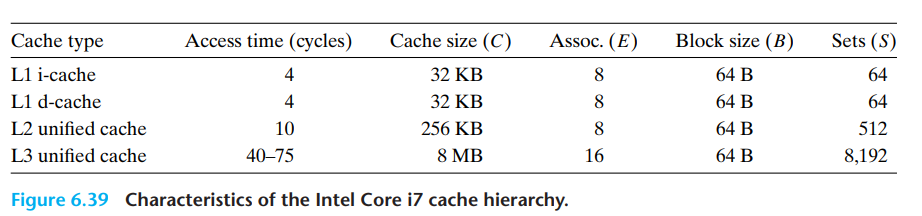
- 注意到cache缓存通常块大小是64字节
- L1 cache访问需要4个时钟周期
- L2 cache访问需要10个时钟周期
- L3 cache访问需要50个时钟周期
3. Cache memories
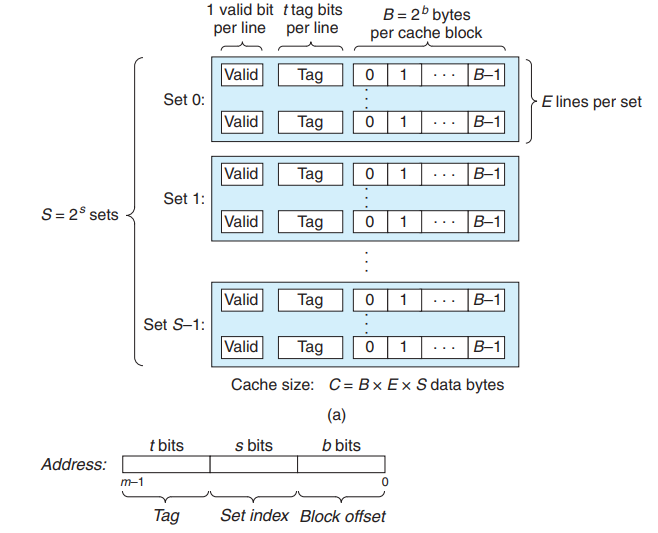
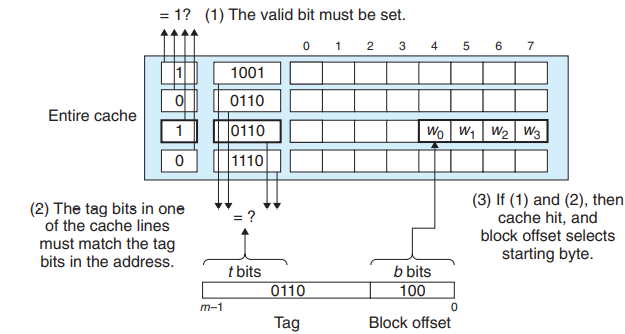
假设每个内存地址为$m$位。高速缓存被组织成$S = 2^s$个高速缓存组(cache set),每个组包括$E$个高速缓存行。每行包括
- $B = 2^b$字节的数据块
- 有效位
- $t = m - s - b$个标记位
因此,高速缓存的结构可以由四元组(S, E, B, m)描述。高速缓存的大小$C$指的是所有块大小之和,不包括有效位和tag,即$C = S * E * B$。
同时$m$位的地址被划分为三个部分如下所示
3.1. 直接映射
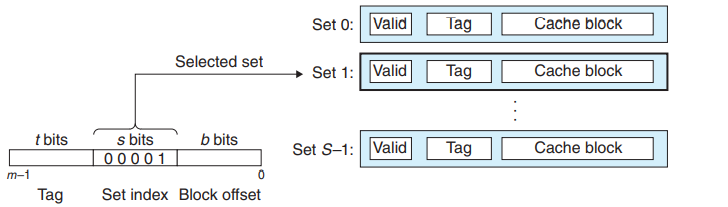
- 直接映射: 每个组只有一行,$E = 1$
- 组选择位(set index): 唯一映射到一个缓存行
- 组选择: 通过$S$位进行选择
- 行匹配: 通过$t$位进行匹配
- 字抽取: 通过$m - s - t$位的值进行偏移
不命中
- 可能会出现抖动(thrash)
3.2. 组相联
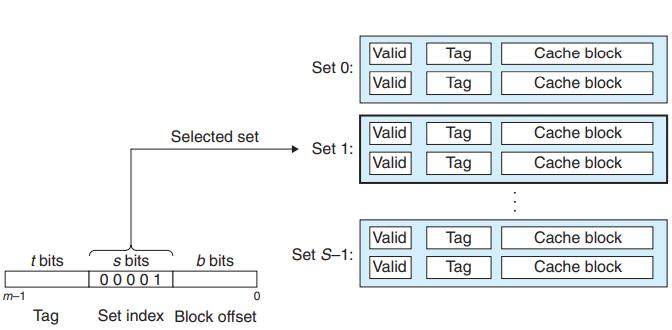
- 组相联: 每个组有$1 < E < \frac{C}{B}$行
- 相联存储器指的是(key,value)存储。组相联指的是多个组的相联存储器。
- 组选择: 通过$S$位进行选择
- 行匹配: $t$位(和标志位)作为键,相当于一个小的相联存储,块作为值进行匹配
- 字抽取
不命中
- 使用替换算法
- LFU: 最不常用,即最近一段时间,引用次数最少
- LRU: 最近最少使用,即最近一段时间,引用时间距离最远
- 性能损失
- 替换策略需要额外的时间和设备,但是越偏向存储层次结构的底层,一次不命中的开销远高于这种额外的时间和设备。
3.3. 全相联
- 全相联: 只有1个组,即$S = 1, s = 0$,行数$E = \frac{C}{B}$
- 由于需要并行匹配多个缓存行,全相联只适合做小的高速缓存,例如TLB。
3.4. 写缓存
写命中
- 直写: 直接写入下一层
- 写回: 需要额外的修改位
写不命中
- 写分配(write-allocate): 先读下一层的块到当前层,然后写入当前层
- 和写回搭配
- 需要额外的一次读操作
- 非写分配(not write-allocate): 直接写入下一层
- 和直写搭配
3.5. 性能参数
- miss rate: 不命中数量 / 引用数量
- hit rate: 1 - miss rate
- hit time: 从高速缓存传送一个字到CPU的时间,组选择、行选择和字选择的时间之和。
- miss penalty: 由于不命中所需要的额外的时间
一些tradeoff
- 高速缓存大小
- 大:命中率大,命中时间(物理限制)长
- 块大小
- 大: 局部性容易利用,命中率容易变大,行数少
- 相联度
- 高: 命中率大, 命中时间长,由于更复杂,不命中处罚变大
- 整体上而言,命中时间占比大而不命中处罚占比小,但是单次命中、不命中时间都变长
- 离CPU近的高速缓存系统,因为命中、不命中相差不大,使用较低的相联度
- 写策略
- 直写可以使用写缓冲区,且非写分配在高层导致的读未命中惩罚不大。
- 写回减少总线传输,允许更多的DMA
- 越底层,写回越多
4. 高速缓存与性能
存储系统读性能测试
- 读吞吐率/读带宽: 一般用MB每秒表示。
下面是测试内存系统读性能的函数
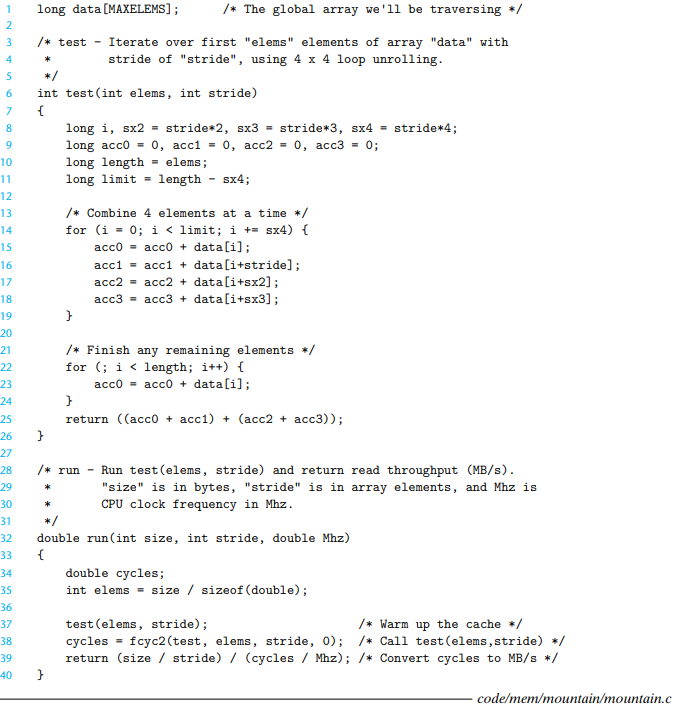
- size: 读取元素的总字节数
- elems: 读取的元素数目
- stride: 读取的两个元素间的步长
- 首先预热(因此有时间局部性),然后通过
fcyc2测试执行周期数
内存山
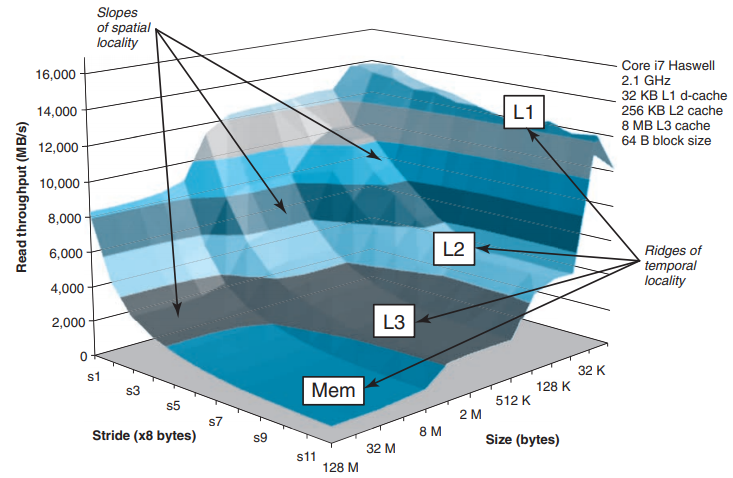
- 工作集越小,时间局部性越好
- 步长越小,空间局部性越好
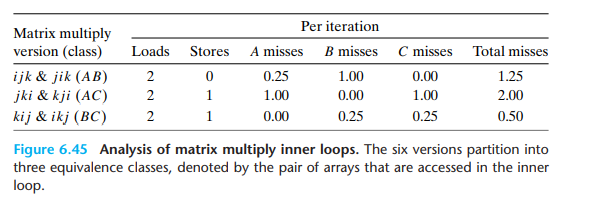
4.1. 综合:重排循环对矩阵乘法效率的影响
- 矩阵乘法中: $C = A_{ik} * B_{kj}$
- 按最内层循环分类,有三种遍历计算方式
- 对i遍历: 内层遍历A的列和C的列
- 对k遍历: 内层同时遍历A的行和B的列
- 对j遍历: 内层遍历B的行和C的行
- 假设
- 数组都是double类型的
- 只有一个高速缓存,块大小为32字节
- 数组大小n很大,一个高速缓存行装不下
- 编译器将局部变量存储在寄存器中,无加载或存储指令的开销

性能统计如下
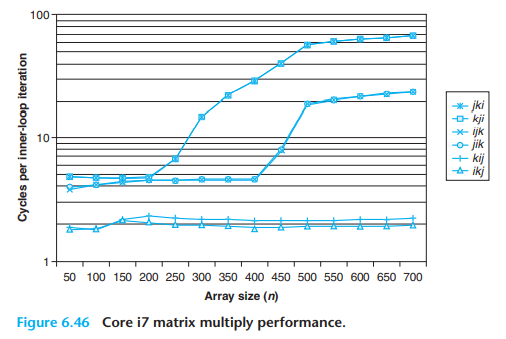
- 随着n的增大,最坏性能和最好性能相差了40倍
- 该案例中和内存访问总数相比,缓存命中率是一个更好的指标。虽然按k迭代的版本内存访问次数减少,但是性能仍比按j迭代的慢
- 随着n的增大,按j迭代的版本下性能变化不大,这是由于core i7预取硬件能够识别步长为1的访问模式
矩阵分块操作
- 假设
- cache block大小为8个doubles
- cache size C « n
对于按k遍历的情况,首次迭代$n/8 + n$次未命中,之后的情况类似。总未命中数为 $9n/8n^2 = (9/8)n^3$
对于分块运算

- $3B^2 < C$
- 让2个输入块和1个输出块都能放入缓存中
- 单个矩阵块有$B^2/8$次未命中
- 首次迭代有$2\frac{n}{B}\frac{B^2}{8}$次未命中(内循环遍历一次的块数乘以每个块的为命中数)
- 总未命中数为$nB/4 * (n/B)^2 = n^3/(4B)$
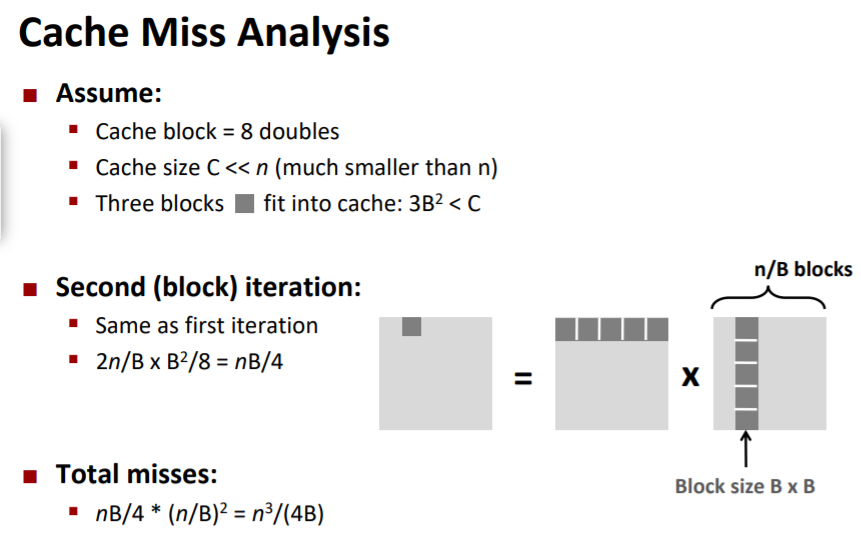
小结
- 无分块: $(9/8)n^3$次未命中
- 分块: $(1/(4B))n^3$次未命中
- 性能差异的原因
- 输入数据为$3n^2$,计算总共需要$2n^3$次(对k遍历,两次内存load操作,无store操作),因此常数因子的上限为2。每一个数组元素被访问了O(n)次,因此幂次3不变。