1. 二进制小数
$b_{m}b_{m-1}…b_1b_0.b_{-1}b_{-2}…b_{-n-1}b_{-n}$
- 对于上面的小数表示法,从小数点往右各个位的权重分别为$2^{-1}, 2^{-2}$等等
- 十进制转换为二进制
- 整数:即除2取余,逆序排列,不停除以二,记录每一次除得到的余数,结果为所有余数的倒序
- 小数:即乘2取整,正序排列,不停乘以二,记录每一次得到的整数部分,结果为所有整数部分的正序
1.1. 二进制小数表示的局限
当位数一定时,二进制小数是一种定点数表示。定点表示有下面两点局限性
- 仅能表示$x/2^k$形式的数
- 能表示的数范围有限,且精度取决于小数点位置的选择
2. IEEE浮点数表示
IEEE 754浮点标准使用 $V = (-1)^sM2^E$ 表示浮点数。
使用三个字段进行编码:
- 符号位:s
- k位阶码(exponent)字段:$e = e_{k-1}e_{k-2}…e_0$
- n位小数(frac)字段:$frac = f_{n-1}f_{n-2}…f_0$
- 注意:这里需要看成定点小数部分
- 精度格式
- 单精度:1位、8位、23位
- 双精度:1位、11位、52位
2.1. 分类
根据exp的值,被编码的值有三种类别:
- 规格化: exp非全0也非全1
- 阶码:$E = e - Bias$
- $Bias = 2^{k-1} - 1$
- e的范围
- 单精度: $1/254 - 127 = -126/127$
- 双精度: $1/2047 - 1023 = -1022/1023$
- 小数:$M = 1 + frac$
- 阶码:$E = e - Bias$
- 非规格化: exp为全0
- 阶码值:$E = 1- Bias$
- 小数:$M = f$
- 和e值为1时的权相同,但是小数部分没有默认的1
- 作用
- 表示0:有+0和-0两种表示
- 表示非常接近0的数
- 特殊值: exp为全1
- 无穷大:frac为全0时,根据符号位分别表示正无穷和负无穷
- NaN:frac非0时,值表示NaN

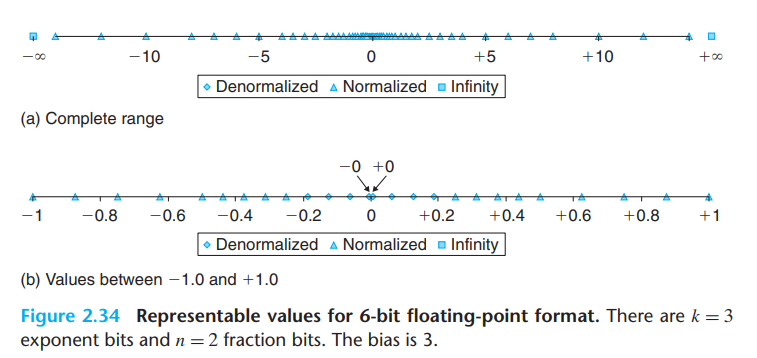
我们可以将能表示的相邻两个数的大小,即阶码部分表示的大小,视作步幅。
- 如下图的坐标轴,浮点数能精确取到的值是非均匀变化的
- 原因在于
- 指数相同的取值以相同的步幅变化
- 指数不相同的取值间变化步幅不同,由于指数爆炸特性,间隔逐渐加大,越靠近0越稠密
- 注意:指数部分为0和为1时由于E均取到$1-2^{k-1}$,因此变化幅度相同
小结
- 值+0.0
- 全0
- 最小正非规格化值
- 小数部分为1,e为0
- 阶码为$2^{1-(2^{k-1} - 1)}$,小数为$2^{-n}$
- 值为$2^{-n-2^{k-1}+2}$
- 最大非规格化值
- 小数部分全1,e为0
- 阶码为$2^{1-(2^{k-1} - 1)}$,小数为$1 - 2^{-n}$
- 值为$(1 - 2^{-n})2^{-n - 2^{k-1} + 2}$
- 最小正规格化值
- 小数部分为0,e为1
- 阶码为$2^{1-(2^{k-1} - 1)}$,小数为$1$
- 值为$2^{-n - 2^{k-1} + 2}$
- 值1.0
- 小数部分为0,e为$2^{k-1}-1$,即阶码部分除了最高位全为1
- 最大规格化值
- 小数部分全1
- 阶码部分除了最低有效位为0其余全1,否则是特殊值
- 小数值为$1-2^{-n} + 1 = 2-2^{-n}$,阶码为$2^{k-1}-1$
- 值为$(2 - 2^{-n})2^{2^{k-1}-1} = (1 - 2^{-n})^{2^{k-1}}$
注意1:阶码部分使用无符号减去偏置,是为了保证和整数类似的数值大小比较的方式。即1越靠前,值越大。
注意2: 阶码部分,从0 ~ 除了最高有效位全1,表示小于等于Bias的部分,和补码表示正好反过来。对于规格化数大于Bias的比小于Bias的多一个。Bias为除了最高有效位全1。
以12345为例解释十进制到IEEE单精度浮点的转换
- 12345的二进制表示为
[11000000111001]共14位 - 左移13位得到科学计数为$1.1000000111001_2*2^{13}$
- 小数部分: 单精度小数部分有23位,因此添10个0得到小数字段
- 阶码部分: 13加上偏移量127得到140
- 符号位: 0
注意:2进制表示下,会保留最高位1之后的部分位。
3. 舍入
- 向最接近的数舍入
- 当有接近的值时,向最接近的舍入
- 当位于两个值的中间时向偶数舍入,使得结果的最低有效位是偶数。这么做的意义在于避免引入统计偏差。
- 对于2进制小数
- 我们将最低有效位的值为0认为是偶数,值1认为是奇数
- 向偶舍入只适用于X..X.YY..Y100…的模式,且最右侧的Y是要被舍入的位置
- 示例: 舍入到百分位
- 10.00011 -> 10.00: 向下
- 10.00110 -> 10.01: 向上
- 10.11100 -> 11.00: 向偶
- 10.10100 -> 10.10: 向偶
4. 浮点运算
将浮点值视作实数,在其上定义运算$\bigodot$,计算的结果为$Round(x\bigodot y)$。当有特殊值时,定义1/0为正无穷,-1/0为负无穷。
浮点运算有如下性质
- 浮点加法
- 由于舍入,浮点加法不具有结合性,编译器因此不能通过结合进行优化
- (3.14 + 1e10) - 1e10 = 0
- 3.14 + (1e10 - 1e10) = 3.14
- 浮点加法满足单调性: 无符号和补码加法不满足
- 若$a\ge b$,则对除了NaN的任何值有$x + a \ge x + b$
- 由于舍入,浮点加法不具有结合性,编译器因此不能通过结合进行优化
- 浮点乘法
- 对乘法封闭
- 可交换
- 由于可能因为舍入失去精度,不可结合
- (1e20 * 1e20) * 1e-20为正无穷
- 1e20 * (1e20 * 1e-20)为1e20
- 对加法不具备分配性
- 1e20 * (1e20 - 1e20) = 0
- 1e20 * 1e20 - 1e20 * 1e20 = NaN
- 单调性:无符号和补码乘法不满足
- 对任意a,b,c,且a,b,c均非NaN有
- $a \ge b, c\ge 0 \rightarrow a * c \ge b * c$
- $a \ge b, c\le 0 \rightarrow a * c \le b * c$
- 若a不是NaN,$a * a \ge 0$
- 对任意a,b,c,且a,b,c均非NaN有
5. C语言浮点运算
- int转换为float,数字不会溢出,但可能舍入
- int或float转换为double,不会溢出也不会舍入,double小数部分有52位所以可以包含
- double转换为float,可能溢出为无穷也可能舍入
- float或者double转换成int,向0舍入,或溢出
- 1.999会被转换成1
- -1.999会被转换成-1
- 溢出情况: 与Intel兼容的处理器指定位模式[1000..0]即TMin为整数不确定值,当无法找到合适的转换值时,使用该值。因此大整数会被溢出为负数。