The increase of processor speed is way faster than memory speed. Caches can help, but definitely not a panacea. What makes it worse is the presence of NUMA arch.
challenge - NUMA multiprocessors:
- remote memory accesses
- cache coherence cost more
- normally directory based cache coherence
idea: by overlapping memory access with computation and other accesses, tolerate latency through prefetching

- benefits
- prefetch early enough: completely hides memory latency
- issue prefetches in blocks
- pipeline the misses
- only the first reference stalls
- prefetch with ownership
- reduces write latency, coherence messages
1. types of prefetching
- large cache blocks
- limitations: spatial locality, false sharing
- hardware-controlled prefetching: hardware can detect simple strided access patterns
- limitations: simple patterns, page boundaries, cache pollution
- software-controlled prefetching
- insert explicit instructions in modern instruction sets
- limitations: instruction overhead?
2. compiler-based prefetching, a.k.a fully-automate prefetch insertion
- access patterns
- arrays, pointers
- goal
- maximize benefit
- minimize overhead
2.1. prefetching concepts
- pre-conditions: address is predictable
- coverage factor: fraction of misses that are prefetched
- unnecessary prefetch: data is already in the cache
- effective prefetch: data prefetched is in the cache when later referenced
- analysis: what to prefetch
- maximize coverage factor
- minimize unnecessary prefetches
- scheduling: when/how to schedule prefetches
- when: a cache miss expect to happen
- minimize overhead per prefetch
注意: 有很多程序已经能够达到很高的cache命中率,因此减少不必要的预取是非常重要的。
2.2. compiler algorithm
- step 1: what to prefetch
- locality analysis
- step 2: instruction scheduling when/how to issue prefetches
- loop splitting
- software pipelining
2.2.1. locality analysis steps
- find data reuse
- prefetch only when memory access suffer cache misses
- 被重用的数据有潜在的达成cache hit的可能,对于能够cache hit的内存访问就不需要再进行预取。
- determine “localized iteration space”
- set of inner loops where the data accessed by an iteration is expected to fit within the cache
- find data locality
- reuse and localized iteration space
2.2.1.1. data reuse
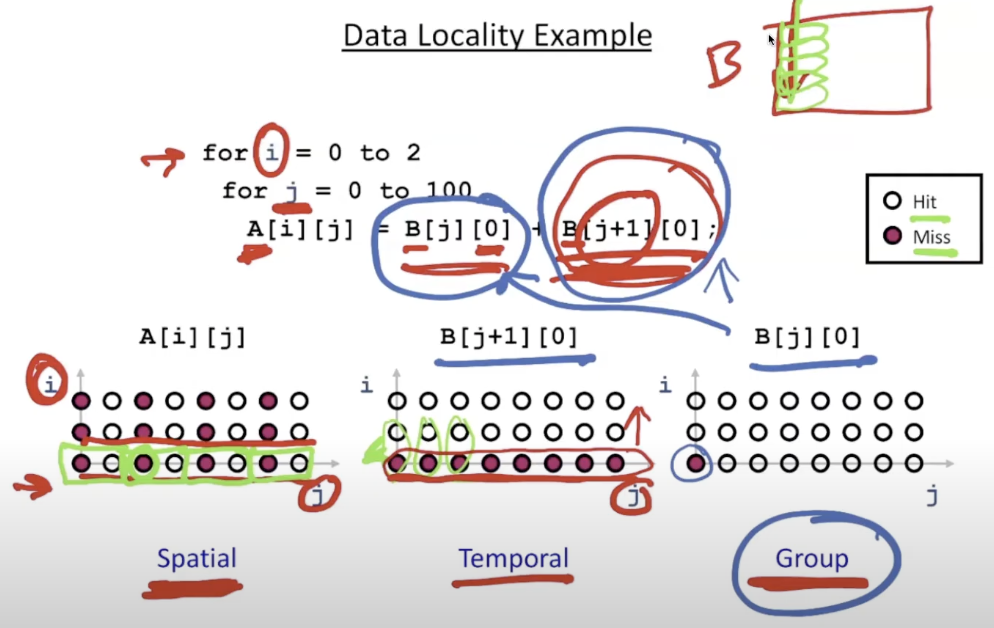
suppose one cache line can hold 2 elements
the graph is called iteration space, x and y axis represents time
- spatial locality: access element in the same cache line
- 对A[i][j]
- temporal locality: access the same element
- 对B[j+1][0]: 上例中对于不同的i(外循环)重用了B数组
- group locality:
- 对B[j][0]: 只在第一次访问时miss,之后的访问因为有B[j+1][0]的存在能够直接hit
2.2.1.2. localized iteration space
- given compiler a parameter about the cache size and the compiler will estimate how much data a loop has and then it will decide if it will be a capacity miss or not
2.2.1.3. find data locality
| locality type | miss instance | predicate |
|---|---|---|
| none | every iteration | true |
| temporal | first iteration | i = 0 |
| spatial | every l iterations (l = cache line size) | (i mod l) = 0 |
对于那些cache miss的内存访问有潜在的预取机会。
2.2.2. schedule
2.2.2.1. loop splitting
- strawman method: insert
IFstatement, if will miss, then prefetch- cost too high
- decompose loops to isolate cache miss instances
loop transmission method
| locality type | loop transformation |
|---|---|
| None | direct prefetch |
| Temporal | Peel out loop i, then insert prefetch |
| Spatial | Unroll loop i by l, then insert prefetch once |
2.2.2.2. software pipelining
- prefetch iterations ahead
- given parameter
- l = memory latency
- s = shortest path through loop body
$Iterations\;Ahead = \lceil\frac{l}{s}\rceil$

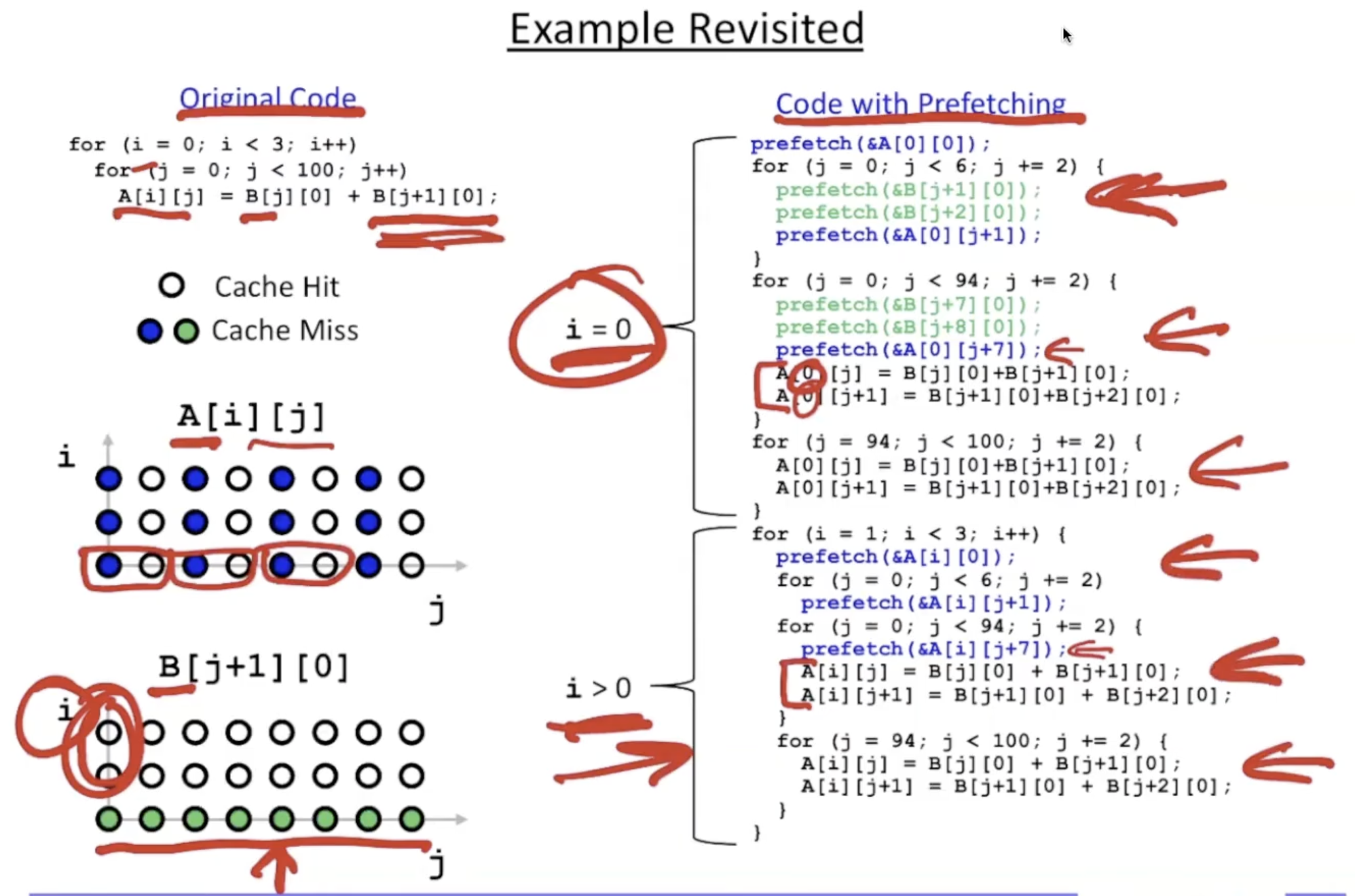
2.2.3. example
2.3. evaluation
performance

effectiveness
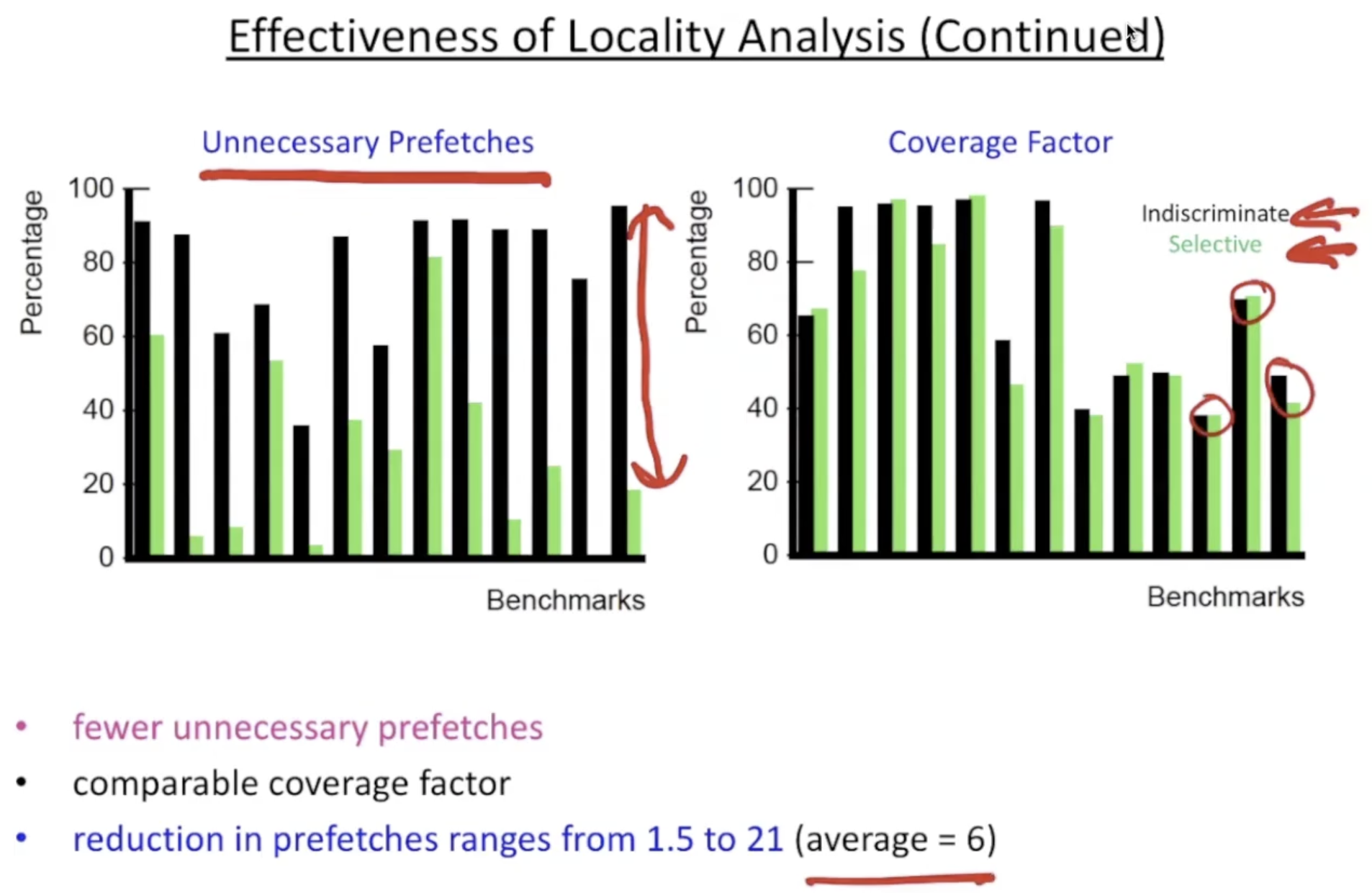
effectiveness of software pipelining

2.4. prefetching indirections
A[index[i]]
- analysis: what to prefetch
- hard to predict whether indirections hit or miss
- in general, just prefetch
- scheduling: when/how to issue prefetches
2.4.1. software pipelining for indirections
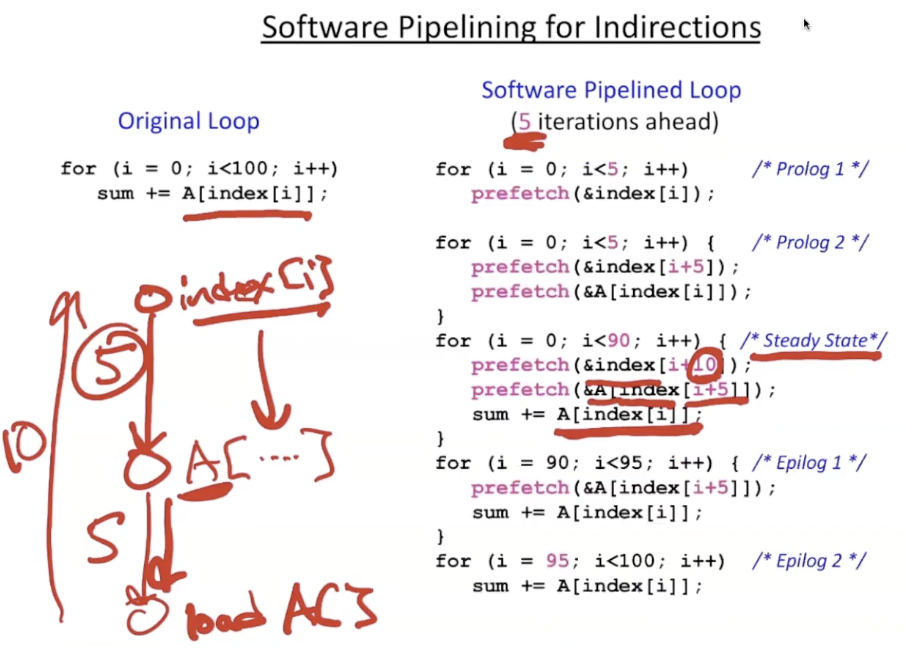
2 level deep pipeline
2.4.2. evaluation
not fetch vs. fetch dense reference vs. fetch dense + indirect reference

3. prefetching for parallel shared-address-space machines
- non-binding prefetches vs binding prefetches: whether the value is determined, in load time or in prefetch time
- binding prefetch: determined in prefetch time, cause stale data
- ex. load into register, may not be correct
- non-binding prefetch: determined in load time, prefetch to cache, may be invalidated
- no restrictions on when prefetches can be issued, the protocol guarantees the correctness of the program, even if we take aggressive strategy
- binding prefetch: determined in prefetch time, cause stale data
- deal with coherence miss
- take into account explicit synchronization
- optimization
- exclusive mode
- ex.
X = X + 1, use readX to load data to decrease synchronization cost - 已经有writer buffer
- 但是隐藏invalidate traffic message
- ex.
- exclusive mode
- analysis
- 减小锁的时间,减小在同步区的时间,因此减小同步时间

we now have synchronization cost
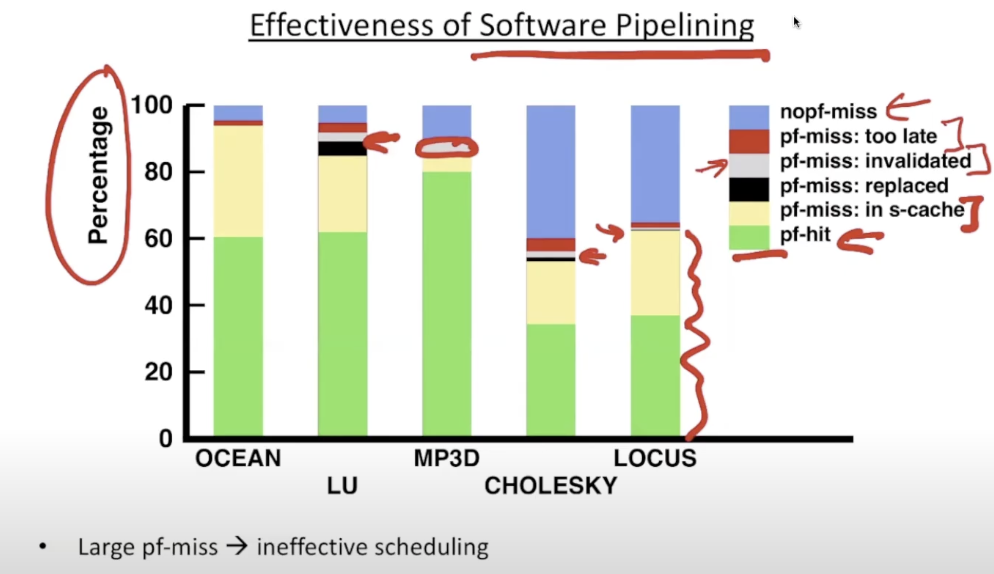
- pf-miss: in s-cache
- good: since can found in the second level cache
- pf-miss: invalidated
- pf-miss: replaced
- pf-miss: too late
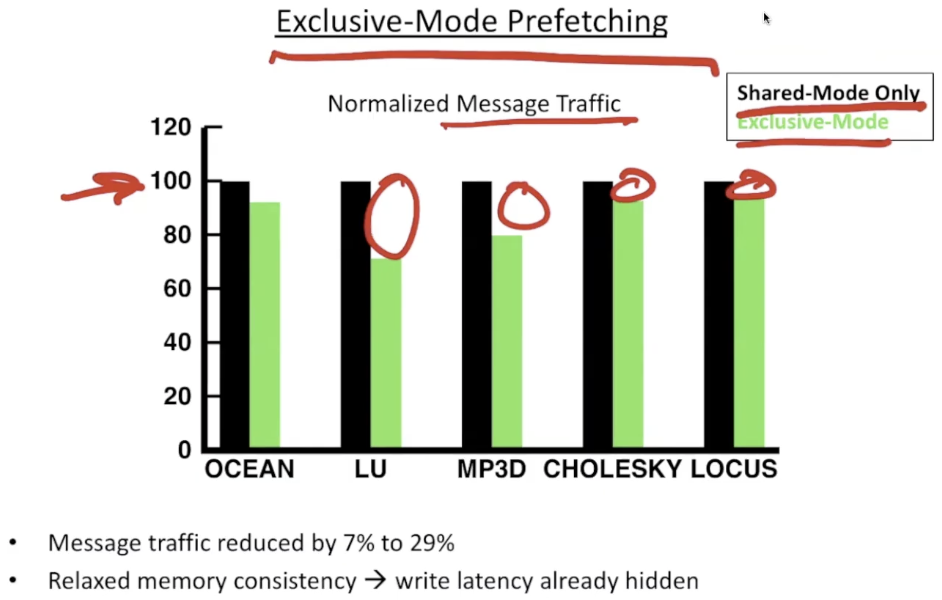
reduce message traffic
4. prefetch for database
4.1. hash join
- build a hash table to index all tuples of the smaller relation
- probe the hash table using all tuples of the larger relation
- bad spatial locality
group prefetching

5. limitations: memory bandwidth

- if already bandwidth-limited, then prefetch can not help
- configuration
- last level cache
- separate memory
- same latency but higher bandwidth
6. prefetch for pointers data structures
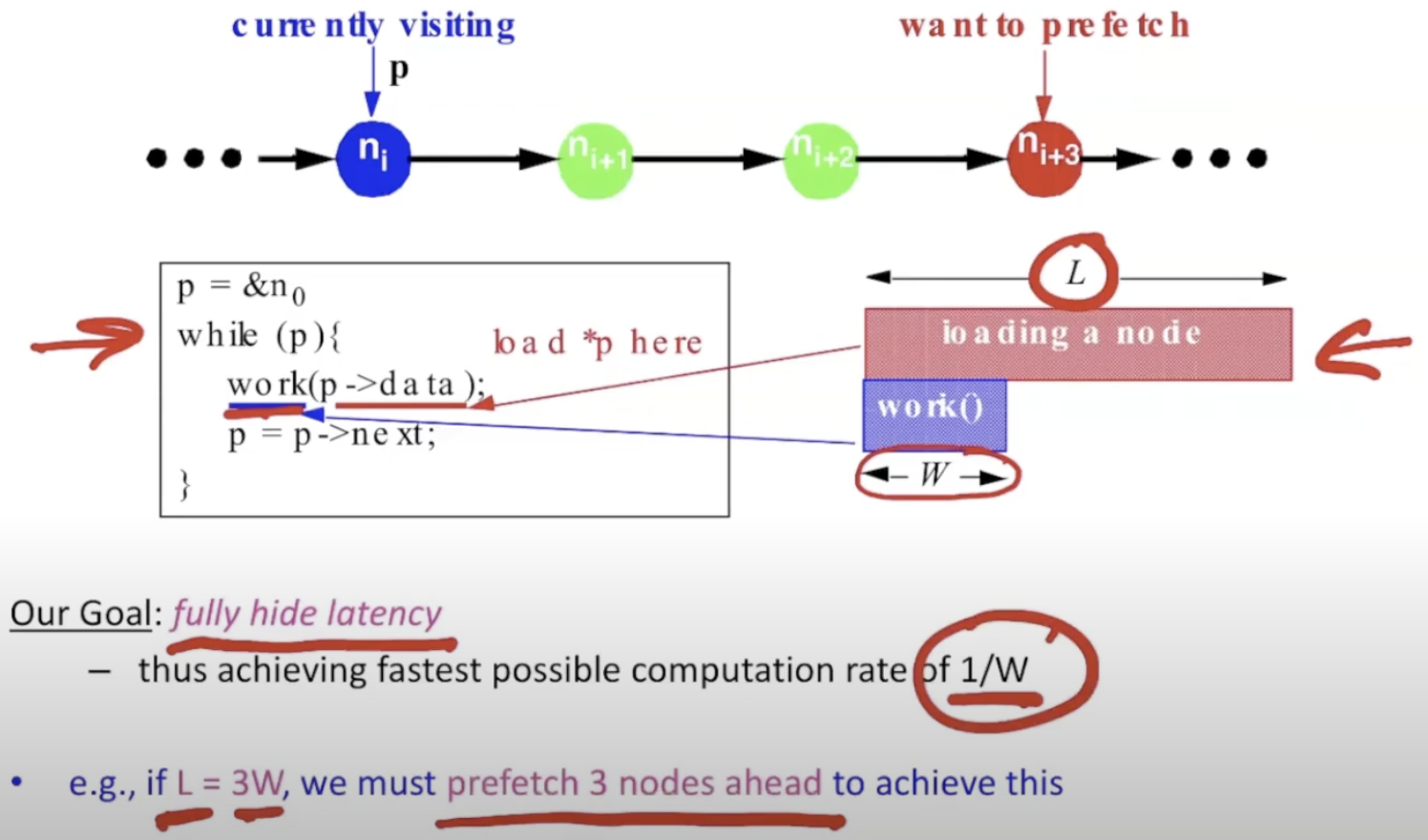
load时间是计算时间的三倍

cache miss + work -> cache miss + work -> …
无预取情况下,计算速率: 1/(L+W). every L+W cycles to process each node.

load current, then can get next pointer and begin load next
预取单个节点,overlap单次load和单次work,计算速率: 1/L。every L cycles to process each node.
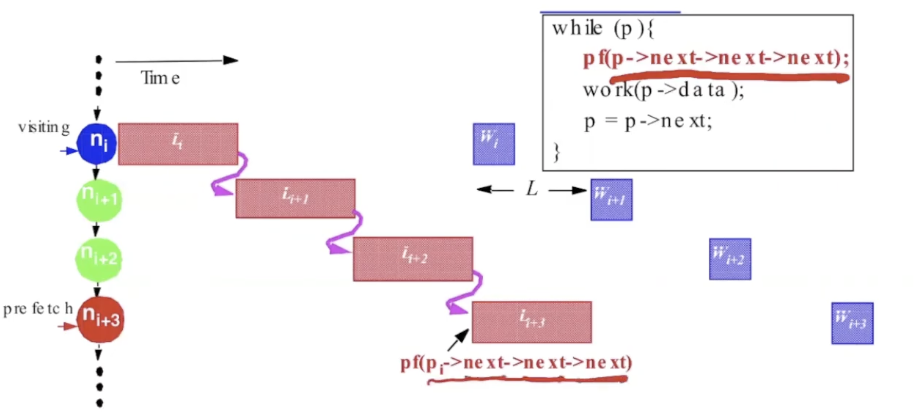
预取三个节点,需要获取三个节点才能开始work: pointer-chasing problem
any scheme which follows the pointer chain is limited to a rate of 1/L.
goal and solution

we want to achieve 1/W computation rate
key:
- $n_i$ needs to know $\&n_{i+d}$ without referencing the d-1 intermediate nodes
proposals
- greedy prefetching
- use existing pointers in $n_i$ to approximate $\&n_{i+d}$
- 预取所有子节点(例如:树)

- history-pointer prefetching
- add new pointers to $n_i$ to approximate $\&n_{i+d}$
- more space and run time pointer construction overhead
注意: 只有重复多次访问该数据结构时才有效。

- data-linearization prefetching
- compute $\&n_{i+d}$ directly from $\&n_i$ (no ptr deref)
- map nodes close in the traversal to contiguous memory